CHƯƠNG 4: PHONON I. DAO ĐỘNG MẠNG

DAO ĐỘNG CỦA TINH THỂ CÓ CƠ SỞ (NỀN) GỒM MỘT NGUYÊN TỬ

Về mặt lí thuyết, tại nhiệt độ không tuyệt đối, các nguyên tử nằm ở vị trí năng lượng thấp nhất của nó mà không chuyển động. Khi nhiệt năng được cung cấp cho tinh thể thì các nguyên tử sẽ dao động xung quanh vị trí cân bằng của chúng. Mỗi nguyên tử hành động như thể nó được gắn với các nguyên tử lân cận bằng một lò xo. Năng lượng này được dự trữ trong tinh thể dưới dạng động năng của các nguyên tử hoặc thế năng giãn nén của lò xo.

Xét dao động đàn hồi của tinh thể có một nguyên tử trong một ô đơn vị tối giản. Chúng ta cần tìm tần số của sóng đàn hồi theo vecto sóng và hằng số đàn hồi.

Nghiệm của phương trình sóng sẽ đơn giản nhất khi sóng truyền theo các hướng [100], [110], và [111] của mạng tinh thể lập phương. Đây là các hướng của cạnh hình hộp, đường chéo ở mặt bên và đường chéo chính.

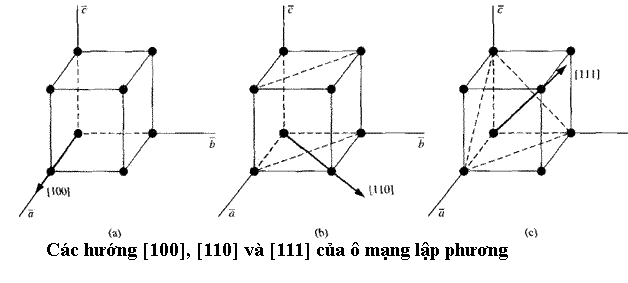
Khi sóng truyền theo một trong những hướng này, toàn bộ mặt phẳng nguyên tử sẽ dịch chuyển hoặc song song (hình 2) hoặc vuông góc với vecto sóng (hình 3). Chúng ta gọi u_s là sự thay đổi vị trí của mặt phẳng s so với vị trí cân bằng của nó. Bây giờ chúng ta xét bài toán một chiều.

Chúng ta giả sử rằng sự dịch chuyển vị trí của mạng so với vị trí cân bằng tỉ lệ với lực đàn hồi; và lực tác dụng lên mặt phẳng s do sự thay đổi vị trí của mặt phẳng s+p tỉ lệ với hiệu những dịch chuyển vị trí của chúng u_s+p – u_s. Để cho ngắn gọn, chúng ta chỉ xét những tương tác gần nhau nhất, với p=±1. Lực tác dụng tổng cộng lên mặt phẳng s do các mặt phẳng s+1 và s – 1 gây ra là:

F_s=C(u_s+1 – u_s) + C(u_s-1 – u_s) (1)

Lực tỉ lệ với sự thay đổi vị trí và biểu thức này có dạng của định luật Hooke.

Hằng số C là hằng số lực giữa những mặt phẳng lân cận gần nhất và sẽ khác nhau đối với các sóng dọc và sóng ngang. Từ nay, để cho thuận tiện, chúng ta sẽ xem C được định nghĩa cho một nguyên tử của mặt phẳng, vì thế F_s là lực tác dụng trên một nguyên tử trong mặt phẳng s. Nghĩa là bây giờ chúng ta chỉ xét một dãy các nguyên tử, giữa các nguyên tử này có tương tác với nhau bằng lực đàn hồi.

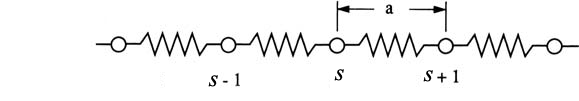
Phương trình chuyển động của một nguyên tử trong mặt phẳng s là:

(2)

ở đây M là khối lượng của nguyên tử.

Nghiệm của phương trình này có dạng:

u_s(t)=uexp(isKa)exp(–iωt), (3)

Suy ra:

u_s±1(t)=uexp[i(s±1)Ka)exp(–iωt)=u_s exp(±Ka) (3’)

ở đây a là khoảng cách giữa các mặt phẳng khi chúng ở tại vị trí cân bằng và K là vecto sóng. Giá trị của a sẽ phụ thuộc vào hướng của K.

Từ (3) suy ra d²u_s/dt²=–ω²u_s, và (2) trở thành

–Mω²u_s=C(u_s+1+u_s–1 –2u_s ) (4)

Thế các số hạng u_s+1, u_s-1, và u_s vào vế phải, ta được:

ω²M=–C[exp(iKa)+exp(–iKa)–2] (5)

Mặt khác

exp(iKa)+exp(–iKa)=2cosKa

nên chúng ta có hệ thức tán sắc ω(K) là:

ω²=(2C/M)(1–cosKa) (7)

Người ta định nghĩa vùng Brillouin thứ nhất là vùng có vecto sóng nằm trong khoảng . Từ (7), chúng ta thấy rằng hệ số góc của đường cong ω theo K sẽ bằng 0 tại biên vùng vì:

dω²/dK=(2Ca/M)sinKa

và dω²/dK(K=±π/a)=(2Ca/M)sin±π=0

Ý nghĩa đặc biệt của vecto sóng phonon nằm ở biên vùng được thể hiện trong công thức (12) bên dưới.

Sử dụng các hệ thức lượng giác, (7) có thể được viết lại là:

ω²=(4C/M)sin²½Ka; ω=(4C/M)^1/2|sin½Ka| (9)

Đồ thị của ω theo K sẽ có dạng như hình 4.

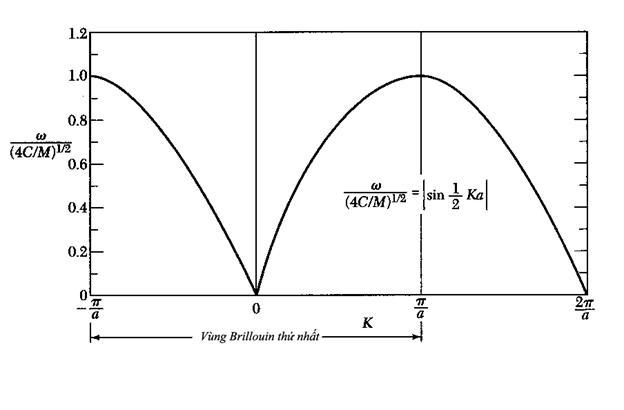
Hình 4: Đồ thị của ω theo K

Vùng Brillouin thứ nhất

Đối với sóng đàn hồi, khoảng giá trị nào của K chứa đựng ý nghĩa vật lí thực sự? Câu trả lời là: Chỉ những giá trị nào của K nằm trong vùng Brillouin thứ nhất. Từ (3) và (3’), tỉ số độ dịch chuyển vị trí của hai mặt phẳng lân cận nhau là:

(10)

Giá trị của pha Ka trong khoảng từ –π đến π chứa tất cả những giá trị độc lập của hàm mũ (điều I). Chúng ta sẽ chứng minh điều này ngay bên dưới.

Nghĩa là, khoảng các giá trị độc lập của K là:

–π ≤ Ka ≤π, hoặc –π/a≤ K≤ π/a

Khoảng này là vùng Brillouin thứ nhất của mạng một chiều. Cực đại của vùng nằm tại K_max=±π/a. Giá trị của K nằm ngoài vùng Brillouin thứ nhất chỉ đơn thuần tạo lại những chuyển động mạng giống như trong vùng Brillouin thứ nhất.

Bây giờ chúng ta sẽ đi chứng minh tỉ lệ độ dịch chuyển vị trí trong vùng Brillouin thứ nhất và ngoài vùng này là như nhau (chứng minh điều I). Xét K nằm ngoài vùng Brillouin thứ nhất (B1). Bằng cách lấy vecto sóng (độ lớn) này trừ đi một số nguyên lần của 2π/a, chúng ta sẽ được một vecto nằm trong vùng B1.Chẳng hạn, chúng ta kí hiệu vecto sóng đó là : , ở đây n là số nguyên. Do đó, tỉ lệ dịch chuyển vị trí trong biểu thức (10) trở thành:

(11)

Bởi vì exp(i2πn)=1. Do đó sự dịch chuyển vị trí luôn luôn có thể được mô tả bởi vecto sóng trong vùng B1. Chúng ta chú ý rằng 2πn/a là vecto mạng đảo bởi vì 2π/a là vecto mạng đảo. Vì thế, bằng cách lấy K trừ cho một vecto mạng đảo thích hợp, chúng ta luôn luôn thu được một vecto sóng tương đương với vecto sóng trong vùng Brillouin thứ nhất.

Tại biên vùng Brillouin K_max=±π/a nên:

u_s=uexp(isKa)=uexp(±isπ)=u(-1)^s. (chúng ta đang khảo sát sóng biến đổi như thế nào trong không gian nên chúng ta sẽ không viết ra thành phần phụ thuộc thời gian) (12)

Nghĩa là nghiệm không biễu diễn sóng chạy mà là sóng đứng.

Những nguyên tử cạnh nhau sẽ dao động ngược pha nhau bởi vì u_s=±u tùy theo s là số nguyên chẵn hay lẻ. Sóng không chuyển động sang phải mà cũng không chuyển động sang trái.

Trường hợp này tương tự như hiện tượng phản xạ Bragg của tia X: khi điều kiện Bragg được thõa mãn thì sóng chạy không truyền trong mạng. Những mặt phẳng cạnh nhau phản xạ tới lui hình thành nên sóng đứng.

Xem lại hiện tượng phản xạ Bragg:

Cực trị của K là K_max=±π/a được tìm ra ở đây thõa mãn định luật Bragg 2dsinθ=nλ.

Thật vậy, K_max=±π/a tương ứng với λ=2a; và chúng ta lại có θ=½π, d=a, n=1, do đó thế vào ta được 2asin½π=2a.

Với tia X, n có thể bằng những số nguyên khác chứ không chỉ bằng 1 bởi vì biên độ của sóng điện từ có nghĩa trong toàn không gian trong khi đó biên độ của độ dịch chuyển vị trí của sóng đàn hồi thường chỉ có nghĩa tại chính nguyên tử đó.

Vận tốc nhóm

Vận tốc nhóm là vận tốc truyền của bó sóng:

Hoặc

(13)

Nghĩa là vận tốc nhóm bằng gradient của tần số đối với K . Đây là vận tốc truyền năng lượng trong môi trường.

Với hệ thức tán sắc (9) thì vận tốc nhóm (hình 6) sẽ là:

(14)

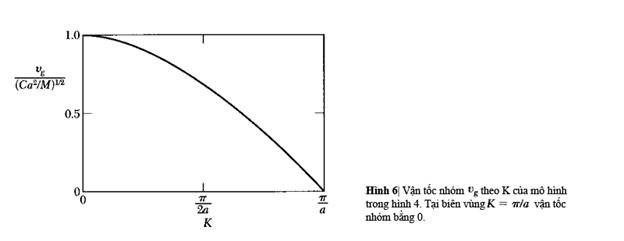
Vận tốc nhóm sẽ bằng 0 tại biên vùng. Ở đây sóng là sóng đứng, như trong (12), và chúng ta suy ra rằng sự truyền vận tốc toàn phần sẽ bằng 0 đối với sóng đứng.

Vận tốc pha

Vận tốc pha là vận tốc lan truyền pha của sóng trong không gian.

υ_ph=ω/K

Xem video (bạn có thấy vận tốc chuyển động của cả bó sóng chậm hơn vận tốc chuyển động của các pha sóng bên trong nó không ?)

Giới hạn bước sóng dài

Khi Ka<<1, chúng ta sẽ có cosKa=1–½(Ka)², do đó hệ thức tán sắc (7) trở thành:

ω²=(C/M)K²a² (15)

Như vậy, ở đây tần số tỉ lệ trực tiếp với vecto sóng trong trường hợp bước sóng dài. Suy ra vận tốc pha và vận tốc nhóm sẽ bằng nhau:

Mặt khác, theo lí thuyết đàn hồi, tốc độ lan truyền của sóng âm thanh trong môi trường liên tục là

Nghĩa là trong trường hợp bước sóng dài thì mạng tinh thể có thể được coi là một môi trường liên tục và lúc này sóng dao động của mạng tinh thể trùng với sóng âm thanh.

Việc rút ra hằng số lực từ thực nghiệm

Trong kim loại, lực hiệu dụng có thể tồn tại trong một khoảng dài và được truyền từ Ion này đến Ion khác qua “biển” electron. Tương tác vẫn còn được tìm thấy giữa những nguyên tử nằm cách xa nhau khoảng 20 mặt phẳng mạng. Do đó, chúng ta có thể xác định khoảng tác dụng của lực từ hệ thức tán sắc (hệ thức này được quan sát từ thực nghiệm). Việc tổng quát hóa hệ thức (7) cho những mặt phẳng p gần nhất sẽ cho ra hệ thức tán sắc có dạng:

(16a)

Bây giờ chúng ta sẽ tìm hằng số lực giữa các mặt phẳng C_p bằng cách nhân cả hai vế với cos(rKa), ở đây r là số nguyên, và lấy tích phân trên khoảng giá trị độc lập của K

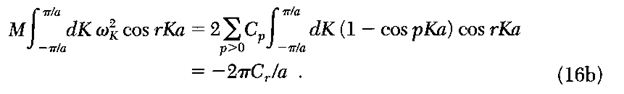
Tích phân sẽ biến mất ngoại trừ tại p=r . Vì thế:

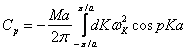(17)

là hằng số lực trên khoảng pa đối với một cấu trúc nền đơn nguyên tử.

HAI NGUYÊN TỬ TRÊN NỀN TỐI GIẢN

Đối với tinh thể có 2 hoặc nhiều nguyên tử trên nền tối giản, hệ thức tán sắc phonon sẽ thể hiện những tính chất mới. Chẳng hạn xét cấu trúc kim cương hoặc NaCl có 2 nguyên tử trên một ô đơn vị tối giản.

Tương ứng với mỗi hướng trong tinh thể sẽ có một chế độ dao động, trong mỗi chế độ dao động ấy hệ thức tán sắc(biểu thức ω theo k) chia thành hai nhánh: nhánh quang học và nhánh âm học như trong hình 7.

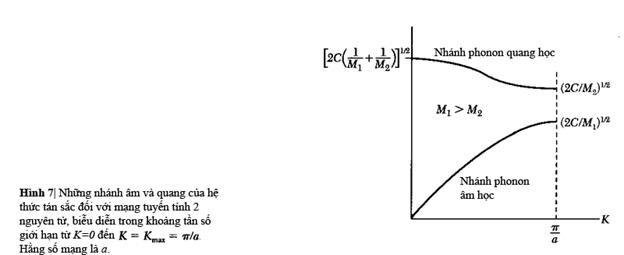
Chúng ta có những chế độ sóng âm ngang (LA) và sóng âm dọc (TA), và sóng quang ngang (LO) và sóng quang dọc (TO).

Nếu có p nguyên tử trong một ô đơn vị tối giản, hệ thức tán sắc sẽ có 3p nhánh: 3 nhánh âm và 3p–3 nhánh quang. Vì thế Ge (hình 8a) và KBr (hình 8b) có 2 nguyên tử trên một ô đơn vị tối giản sẽ có 6 nhánh: một nhánh âm dọc, một nhánh quang dọc, hai nhánh âm ngang và 2 nhánh quang ngang.

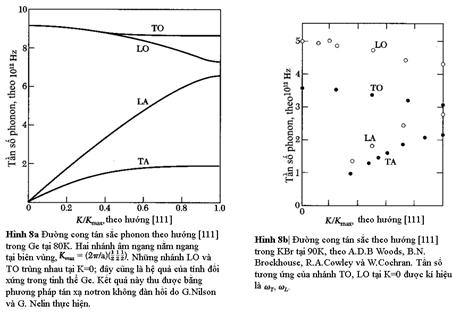
Số nhánh phụ thuộc vào số bậc tự do của nguyên tử. Với p nguyên tử trên một ô đơn vị tối giản và N ô đơn vị tối giản thì sẽ có tổng cộng là pN nguyên tử. Mỗi nguyên tử có ba bậc tự do theo các hướng x, y, z. Vậy tổng số bậc tự do của tinh thể là 3pN. Đối với một vùng Brillouin, số giá trị được phép của K ở một nhánh là N (Điều này được chứng minh bằng cách áp dụng điều kiện biên tuần hoàn vào mô hình tinh thể có thể tích V, trong đó có một giá trị của K trong thể tích (2π)³/V của không gian Fourier). Vì thế, những nhánh âm dọc và 2 nhánh âm ngang có tổng cộng 3N chế độ, do đó chiếm tổng cộng 3N bậc tự do. Số bậc tự do còn lại là (3p – 3)N được dành cho các nhánh quang học.

Chúng ta xét một tinh thể lập phương với những nguyên tử có khối lượng M₁ nằm ở một tập hợp mặt phẳng và những nguyên tử có khối lượng M₂ nằm trên những mặt phẳng xen kẻ với mặt phẳng đầu tiên (Hình 9).

Xem video

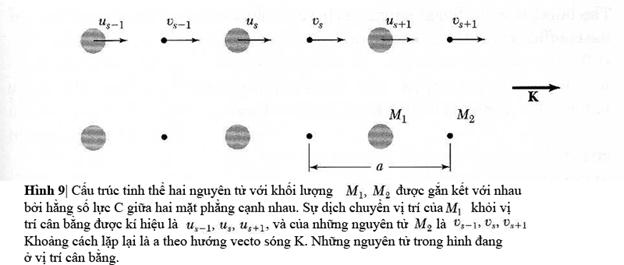
Không nhất thiết khối lượng phải khác nhau, nhưng hoặc là hằng số lực, hoặc các khối lượng sẽ phải khác nhau nếu hai nguyên tử của nền ở những mặt phẳng không tương đương. Đặt a là khoảng cách lặp lại của mạng theo hướng vuông góc với mặt phẳng mạng đang xét. Chúng ta sẽ giải bài toán trong đó sóng truyền theo những hướng đối đối xứng sao cho mỗi mặt phẳng chỉ chứa một loại ion; những hướng này có thể là hướng [111] trong cấu trúc NaCl hoặc hướng [100] trong cấu trúc CsCl.

Chúng ta sẽ viết phương trình chuyển động với giả thuyết rằng mỗi mặt phẳng chỉ tương tác với những mặt phẳng lân cận gần nhất của nó và hằng số lực giữa các cặp mặt phẳng lân cận gần nhất bằng nhau. Dựa vào hình 9, chúng ta thu được:

(18)

Chúng ta tìm nghiệm dưới dạng sóng chạy với các biên độ u, υ khác nhau giữa những mặt phẳng lân cận nhau:

u_s=uexp(isKa)exp(-iωt); υ_s=υexp(isKa)exp(-iωt). (19)

Chúng ta định nghĩa a trong hình 9 là khoảng cách giữa những mặt phẳng cùng loại gần nhau nhất chứ không phải khoảng cách giữa các mặt phẳng lân cận gần nhất.

Thế (19) vào (18), chúng ta có:

–ω²M₁u=Cυ[1+exp(–iKa)]–2Cu;

–ω²M₂υ=Cu[exp(iKa)+1]–2Cυ. (20)

Phương trình thuần nhất tuyến tính có nghiệm chỉ nếu định thức của nó bằng 0:

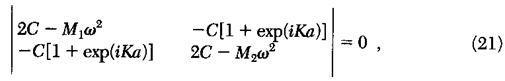
Hoặc:

Chúng ta có thể giải phương trình này để tìm ω², nhưng sẽ đơn giản hơn nếu xét các trường hợp giới hạn Ka<<1 và Ka=±π tại biên vùng. Khi Ka nhỏ (nghĩa là bước sóng rất dài) chúng ta có

, và hai nghiệm là:

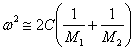(nhánh quang học); (23)

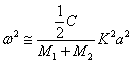(nhánh âm học); (24)

Phạm vi của vùng Brillouin thứ nhất là –π/a ≤k ≤ π/a, ở đây a là khoảng cách lặp lại của mạng. Tại K_max=±π/a nghiệm là:

ω²=2C/M₁; ω²=2C. (25)

Sự phụ thuộc của ω theo K được biễu diễn trong hình 7 cho trường hợp M₁>M₂.

Sự thay đổi vị trí của hạt trong nhánh âm ngang (TA) và nhánh quang ngang (TO) được biễu diễn trong hình 10.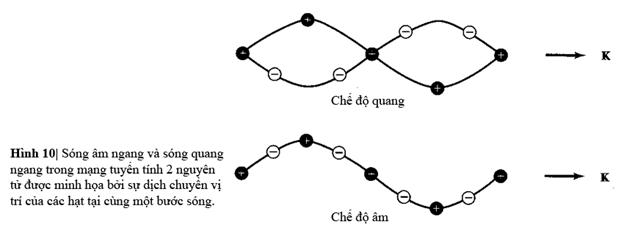

Video sau sẽ mô tả chuyển động của các nguyên tử ở nhánh âm (Acoustic mode) và nhánh quang (Optical mode). Những chấm màu đỏ và màu xanh đại diện cho hai loại nguyên tử khác nhau. Click tại đây

Làm thí nghiệm:

Mô tả: Trong thí nghiệm này, chúng ta sẽ khảo sát sự thay đổi của đường cong tán sắc, của chế độ dao động theo tỉ số khối lượng và tích Ka trong mạng chứa nền gồm 2 nguyên tử khác loại (trong thí nghiện K được kí hiệu là k). Đường thẳng màu xanh lá cây thẳng đứng cho biết sự thay đổi giá trị của ka. Để thay đổi khối lượng, chúng ta sẽ kéo nút hình chữ nhật trong panel có tên là Mass ratio (tỉ số khối lượng giữa của 2 nguyên tử). Để thay đổi giá trị của ka chúng ta kéo nút hình chữ nhật trong panel ka.

Các thuật ngữ tiếng Anh:

· Stop: dừng

· Start: bắt đầu

· Acoustic mode: chế độ dao động âm

· Optical mode: chế độ dao động quang

Thực hiện:

Dành cho máy có Java

Thế (23) vào (20), đối với nhánh quang tại K=0, chúng ta tìm được:

(26)

Những nguyên tử dao động ngược pha nhau nhưng tâm khối của chúng đứng yên. Nếu hai nguyên tử mang điện tích trái dấu, như trong hình 10, chúng ta có thể kích thích chuyển động loại này bằng điện trường của sóng ánh sáng, vì thế nhánh này được gọi là nhánh quang. Đối với giá trị K bất kì, tỉ số u/υ sẽ là số phức theo các phương trình trong (20).

Đối với nhánh âm, khi K=0 thì u=υ. Những nguyên tử (và khối tâm của chúng) di chuyển cùng nhau như trong dao động âm ở bước sóng dài vì thế nhánh này được gọi là nhánh âm.

Xem hình dưới đây

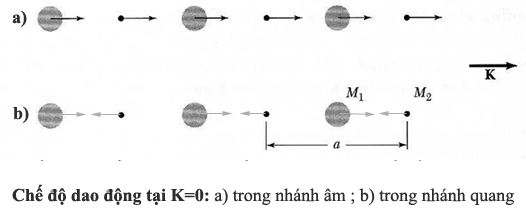
Nghiệm dạng sóng không tồn tại đối với những tần số như thế. Đối với những tần số này, nghiệm có dạng: (2C/M₁)^1/2 và (2C/M₂)^1/2. Đây là tính chất đặc trưng của sóng đàn hồi trong mạng đa nguyên tử. Có một khe tần số tại biên của vùng Brillouin thứ nhất K_max=±π/a.

SỰ LƯỢNG TỬ HÓA SÓNG ĐÀN HỒI

Năng lượng của dao động mạng bị lượng tử hóa. Lượng tử năng lượng này được gọi là phonon, tương tự với lượng tử năng lượng của trường điện từ là photon. Năng lượng của một chế độ dao động đàn hồi với tần số góc ω khi nó được kích thích đến trạng thái lượng tử n là:

(27)

Số hạng là năng lượng điểm không của chế độ. Nó xuất hiện ở cả phonon và photon do chúng tương đương với dao động tử điều hòa lượng tử tần số . Đối với dao động tử điều hòa, trị riêng năng lượng cũng là . Lí thuyết lượng tử của phonon được xây dựng trong phụ lục C.

Chúng ta có thể lượng tử hóa bình phương trung bình của biên độ phonon. Xét chế độ sóng đứng của biên độ

u=u₀cos(Kx)cos(ωt)

Ở đây u là sự dịch chuyển của yếu tố thể tích so với vị trí cân bằng của nó đặt tại điểm x trong tinh thể. Cũng như đối với bất kì dao động tử điều hòa nào, khi lấy trung bình theo thời gian, năng lượng trong chế độ bằng một phần hai động năng và một phần hai thế năng. Mật độ động năng là , ở đây là khối lượng riêng. Trong tinh thể có thể tích V, tích phân theo thể tích của động năng là . Động năng trung bình theo thời gian là:

(28)

vì <sin²ωt>=1/2. Bình phương biên độ của chế độ dao động là:

(29)

Biểu thức này thiết lập mối quan hệ giữa độ dịch chuyển vị trí với sự chiếm phonon ở mức lượng tử thứ n của chế độ.

Dấu của ω là gì? Phương trình chuyển động (chẳng hạn như (2)) là phương trình của ω², và nếu đây là đại lượng dương thì ω có thể có dấu + hoặc –. Nhưng năng lượng của phonon phải dương, vì thế sẽ thuận tiện và hợp lí hơn khi xem ω dương. Nếu cấu trúc tinh thể không ổn định thì ω² sẽ âm và ω là số ảo.

ĐỘNG LƯỢNG PHONON

Một phonon có vecto sóng K sẽ tương tác với những hạt chẳng hạn như photon, nơtron, electron như thể nó có động lượng ћK. Tuy nhiên, phonon không mang động lượng thực.

Nguyên nhân phonon trong mạng không mang động lượng thực là tọa độ phonon (ngoại trừ K=0) liên quan đến những tọa độ tương đối của các nguyên tử. Vì thế trong phân tử hidro chẳng hạn, tọa độ dao động giữa các hạt nhân r₁–r₂ là tọa độ tương đối và không mang động lượng. Tọa độ của tâm khối ½(r₁+r₂) tương ứng với chế độ đồng nhất K=0 và có thể mang động lượng.

Trong tinh thể tồn tại quy tắc lựa chọn vecto sóng cho những dịch chuyển giữa những trạng thái lượng tử. Trong chương 2, chúng ta thấy rằng tán xạ đàn hồi của photon tia X qua mạng tinh thể tuân theo quy tắc chọn lựa vecto sóng:

+ G (30)

ở đây G là vecto của mạng đảo, k là vecto sóng của photon tới, và là vecto sóng của photon tán xạ. Trong quá trình phản xạ, toàn bộ tinh thể sẽ giật lùi với động lượng , nhưng động lượng ở chế độ đồng nhất này hiếm khi được xem xét rõ ràng.

Phương trình (30) là ví dụ về định luật vecto sóng toàn phần của những sóng tương tác được bảo toàn trong mạng tuần hoàn, với việc cộng vào vecto mạng đảo G. Động lượng thực sự của toàn bộ hệ thống luôn luôn được bảo toàn. Nếu tán xạ photon không đàn hồi tạo ra phonon có vecto sóng K thì quy tắc chọn lựa vecto sóng trở thành

. (31)

Nếu phonon K được hấp thụ trong quá trình này, chúng ta thay bằng hệ thức

(32)

Hệ thức (31) và (32) là sự mở rộng của hệ thức (30).

TÁN XẠ PHONON KHÔNG ĐÀN HỒI

Hệ thức tán sắc phonon ω(K) thường được xác định trong thực nghiệm bằng phương pháp tán xạ nơtron không đàn hồi với sự phát hoặc hấp thụ một phonon. Nơtron sẽ tương tác với hạt nhân nguyên tử. Động năng của quá trình tán xạ chùm nơtron bởi tinh thể được mô tả bằng quy tắc chọn lựa vecto sóng tổng quát:

, (33)

và thõa mãn định luật bảo toàn năng lượng . Ở đây K là vecto sóng của phonon được tạo ra (+) hoặc hấp thụ (–) trong quá trình tán xạ, và G là vecto mạng đảo. Đối với phonon, chúng ta chọn G sao cho K nằm trong vùng Brillouin thứ nhất.

Động năng của nơtron tới là p²/2M_n, ở đây M_n là khối lượng của nơtron. Động lượng p bằng ћk , ở đây k là vecto sóng của nơtron. Vì thế ћ²k²/2M_n là động năng của nơtron tới. Nếu là vecto sóng của nơtron tán xạ, năng lượng của nơtron tán xạ sẽ là . Theo định luật bảo toàn năng lượng:

ở đây ћω là năng lượng của phonon được tạo ra hoặc hấp thụ trong quá trình.

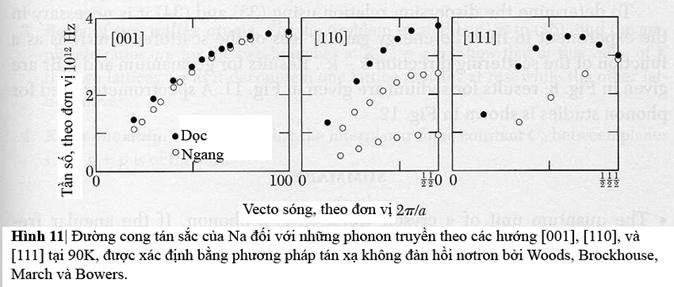
Để xác định hệ thức tán sắc bằng biểu thức (33) và (34), trong thực nghiệm cần tìm ra năng lượng thu được hoặc mất đi của nơtron tán xạ như hàm theo hướng tán xạ . Kết quả cho Ge và KBr được cho trong hình 8; kết quả đối với Na được cho trong hình 11. Phổ kế dùng để nghiên cứu phonon được cho trong hình 12.