![]()
*2.4|
MỞ RỘNG LÍ THUYẾT SÓNG CHO NHỮNG NGUYÊN TỬ
 Ở
trên, chúng ta đã xét một vài hàm thế năng một chiều
và đã giải phương trình sóng Schrodinger độc lập
thời gian để thu được hàm xác suất tìm hạt
tại những vị trí khác nhau. Bây giờ xét hàm thế của
nguyên tử một electron, hoặc Hydro. Chúng ta sẽ không
đi vào giải bài toán cụ thể mà chỉ ghi nhận
và rút ra nhận xét về hàm sóng và các mức năng lượng.
Ở
trên, chúng ta đã xét một vài hàm thế năng một chiều
và đã giải phương trình sóng Schrodinger độc lập
thời gian để thu được hàm xác suất tìm hạt
tại những vị trí khác nhau. Bây giờ xét hàm thế của
nguyên tử một electron, hoặc Hydro. Chúng ta sẽ không
đi vào giải bài toán cụ thể mà chỉ ghi nhận
và rút ra nhận xét về hàm sóng và các mức năng lượng.
2.4.1
Nguyên tử một electron
Hạt nhân là một
proton mang điện dương nặng và electron là một
hạt mang điện âm nhẹ. Theo lí thuyết Bohr cổ
điển, electron quay xung quanh hạt nhân. Hàm thế do
tương tác Coulomb giữa proton và electron là:
![]() (2.63)
(2.63)
ở đây e là
độ lớn của điện tích đơn vị
và ![]() là hằng số điện môi chân không.
Hàm thế này dẫn đến bài toán ba chiều trong hệ
tọa độ cầu.
là hằng số điện môi chân không.
Hàm thế này dẫn đến bài toán ba chiều trong hệ
tọa độ cầu.
Chúng ta có thể tổng quát hóa phương
trình sóng Schrodinger cho trường hợp ba chiều bằng
cách viết
![]() (2.64)
(2.64)
ở đây ![]() là toán tử
Laplace và phải được viết trong hệ tọa
độ cầu cho trường hợp này. m0 là khối lượng
nghỉ của electron. Trong hệ tọa độ cầu,
phương trình Schrodinger có thể được viết
là:
là toán tử
Laplace và phải được viết trong hệ tọa
độ cầu cho trường hợp này. m0 là khối lượng
nghỉ của electron. Trong hệ tọa độ cầu,
phương trình Schrodinger có thể được viết
là:
![]() (2.65)
(2.65)
Nghiệm của phương trình (2.65) có thể
được xác định bằng phương pháp tách
biến. Chúng ta có thể giả sử rằng nghiệm của
phương trình sóng độc lập thời gian có thể
được viết dưới dạng:
![]() (2.66)
(2.66)
ở đây R, ![]() và
và ![]() là hàm theo r,
là hàm theo r, ![]() và
và ![]() . Thế dạng này của nghiệm vào
phương trình (2.65), chúng ta sẽ thu được
. Thế dạng này của nghiệm vào
phương trình (2.65), chúng ta sẽ thu được
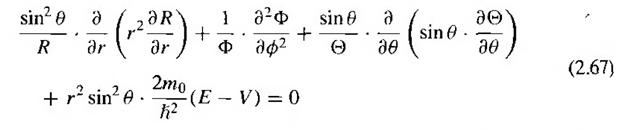
Chúng ta thấy rằng số hạng thứ
2 trong phương trình (2.67) là hàm chỉ phụ thuộc
vào ![]() , trong khi tất cả các hệ số
khác là hàm phụ thuộc vào r
và
, trong khi tất cả các hệ số
khác là hàm phụ thuộc vào r
và ![]() . Do đó, chúng ta có thể viết
. Do đó, chúng ta có thể viết
![]() (2.68)
(2.68)
ở đây m là hằng
số tách biến. Nghiệm của phương trình (2.68)
có dạng
![]() (2.69)
(2.69)
Bởi vì hàm sóng
phải đơn trị nên m
phải là số nguyên, hoặc
![]() (2.70)
(2.70)
Hợp nhất hằng số tách biến,
chúng ta có thể tách thêm những biến ![]() và r và tạo ra thêm hai hằng số
tách biến l và n. Những hằng số tách
biến n, l, m được
gọi là những số lượng tử và mối liên hệ
giữa chúng là
và r và tạo ra thêm hai hằng số
tách biến l và n. Những hằng số tách
biến n, l, m được
gọi là những số lượng tử và mối liên hệ
giữa chúng là
n= 1, 2, 3,…..
l= n–1, n–2, n–3,
….,0 (2.71)
m= –l,…,0,…..+l
Ví
dụ: n=1; l=0; m=0
n=2;
l=0,1; m=0 (đối với
l=0), m=–1, 0, +1 (đối với l=1)
n=3;
l=0, 1, 2; m=0 (đối với l=0), m=–1, 0, 1 (đối với
l=1), m=–2, –1, 0, 1, 2 (đối với l=2)
………………
Mỗi tập hợp
các số lượng tử tương ứng với một
trạng thái lượng tử mà electron có thể chiếm.
Năng lượng electron có thể viết
dưới dạng
![]() (2.72)
(2.72)
ở đây n là số lượng tử.
Năng lượng âm nghĩa là electron liên kết với hạt
nhân và chúng ta lại thấy rằng năng lượng của electron
liên kết bị lượng tử hóa. Nếu năng
lượng trở thành dương thì electron sẽ không
còn là hạt liên kết và năng lượng toàn phần của
nó sẽ không còn bị lượng tử hóa. Bởi vì tham
số n trong phương
trình (2.72) là số nguyên, nên năng lượng toàn phần
của electron chỉ có thể nhận những giá trị
rời rạc. Năng lượng bị lượng tử
hóa một lần nữa chính là kết quả của hạt
liên kết trong một vùng không gian xác định.
Nghiệm của phương trình sóng có thể
được kí hiệu là ψnlm,
ở đây n,l,m là những
số lượng tử khác nhau. Đối với trạng
thái năng lượng thấp nhất , n=1, l=0 và m=0, và hàm
sóng là:
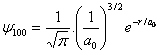 (2.73)
(2.73)
Hàm này đối
xứng cầu, trong đó
![]() (2.74)
(2.74)
Và bằng bán kính
Bohr.
Hàm mật độ xác suất theo r, hoặc
xác suất tìm thấy electron tại một khoảng
nào đó từ hạt
nhân tỉ lệ với tích ψ100.ψ*100
và với thể tích vi phân của vỏ xung quanh hạt
nhân. Hàm mật độ xác suất đối với trạng
thái năng lượng thấp nhất được vẽ
trong hình 2.10a. Khoảng cách có xác suất lớn nhất từ
hạt nhân là tại r=a0.
Điều này giống với lí thuyết Bohr. Xét hàm xác suất
đối xứng cầu này, bây giờ chúng ta có thể
hình thành khái niệm đám mây electron, hoặc những mức
năng lượng bao quanh hạt nhân thay vì những quỹ
đạo rời rạc của hạt quanh hạt nhân.
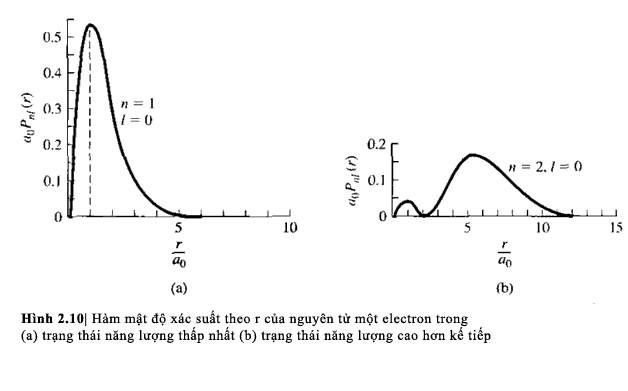
Hàm mật độ xác suất theo r của
hàm sóng đối xứng cầu cao hơn tiếp theo
tương ứng với n=2,
l=0 và m=0 được biễu diễn trong hình 2.10b.
Hình này biểu diễn ý tưởng về những mức
năng lượng cao hơn tiếp theo của electron. Mức
năng lượng thứ hai ở tại bán kính tính từ
hạt nhân lớn hơn mức năng lượng thứ
nhất. Như được chỉ ra trong hình, mặc dù
vẫn còn một xác suất nhỏ để electron tồn
tại ở những bán kính nhỏ hơn. Đối với
trường hợp n=2 và l=1 có 3 trạng thái khả dĩ
tương ứng với 3 giá trị được phép của
số lượng tử m. Những hàm sóng này không còn đối
xứng cầu nữa.
Hãy xem ở trạng thái n=3, l=1, m=0, electron trong nguyên tử hidro chuyển động như thế nào
Hãy xem ở trạng
thái n=3, l=1, m=1, electron trong nguyên tử hidro chuyển động
như thế nào
Mặc dù chúng ta đã không đi sâu vào những
chi tiết toán học của bài toán nguyên tử một
electron nhưng ba kết quả sau đây là quan trọng và
được dùng trong phân tích vật liệu bán dẫn. Thứ nhất là nghiệm của
phương trình sóng Schrodinger một lần nữa mang
đến hàm phân bố electron như nó được giải
với những hàm thế đơn giản hơn. Trong
quá trình xây dựng lí thuyết vật lí bán dẫn trong
chương sau, chúng ta cũng sẽ xét hàm phân bố
electron. Kết quả thứ
hai là sự lượng tử hóa những mức
năng của electron liên kết. Thứ ba là khái niệm về số lượng
tử và những trạng thái lượng tử, nó
được rút ra từ phương pháp tách biến.
Chúng ta sẽ xét lại khái niệm này trong phần tiếp
theo và trong những chương sau khi nghiên cứu vật
lí bán dẫn.
2.4.2
Bảng tuần hoàn
Phần đầu
của bảng tuần hoàn các nguyên tố hóa học có thể
được xác định bằng cách dùng kết quả
của nguyên tử một electron cùng với 2 khái niệm nữa.
Khái niệm thứ nhất
là spin của electron. Electron có momen động lượng
nội tại, hoặc spin. Nó bị lượng tử hóa
và có thể nhận một trong hai giá trị khả dĩ.
Spin được kí hiệu bởi số lượng tử
s, nó có giá trị bằng +1/2 hoặc –1/2. Bây giờ chúng ta có bốn số lượng
tử cơ bản là n,l,m
và s.
Khái niệm thứ
hai là nguyên lí loại trừ Pauli. Nguyên lí loại trừ
Pauli phát biểu rằng trong bất kì hệ thống nào
(nguyên tử, phân tử, hoặc tinh thể), không có 2
electron nào có cùng trạng thái lượng tử. Trong nguyên tử,
nguyên lí loại trừ Pauli muốn nói rằng không có hai
electron nào có cùng tập hợp các số lượng tử.
Chúng ta sẽ thấy rằng nguyên lí loại trừ Pauli cũng
là một nhân tố quan trọng trong việc xác định
phân bố của electron vào những trạng thái năng
lượng có sẵn trong tinh thể.
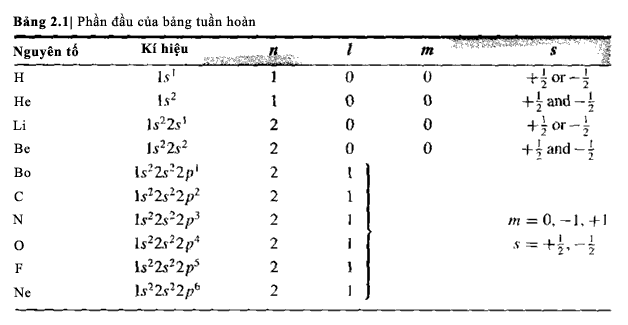
Bảng 2.1 biễu diễn vài nguyên tử
đầu tiên của bảng tuần hoàn. Với nguyên tử
thứ nhất, Hidro, chúng ta có một electron ở trạng
thái năng lượng thấp nhất ứng với n=1. Từ phương trình
(2.71) cả hai số lượng tử l và m phải bằng
0. Tuy nhiên, electron có thể nhận giá trị spin là +1/2 hoặc –1/2. Đối với Heli, hai electron có thể tồn
tại ở mức năng lượng thấp nhất.
Đối với trường hợp này l=m=0, vì vậy bây giờ cả hai trạng thái
spin của electron bị chiếm và mức năng lượng
thấp nhất đầy. Hoạt động hóa học
của một nguyên tố được xác định chủ
yếu dựa vào các electron hóa trị hoặc các electron
ngoài cùng. Bởi vì mức năng lượng hóa trị của
He đầy nên nó sẽ không tương tác với các
nguyên tố khác và là nguyên tố khí trơ.
Nguyên tố thứ 3 Li có 3 electron. Electron thứ
3 phải được sắp vào trong mức năng
lượng thứ 2 tương ứng với n=2, số
lượng tử l có thể là 0 hoặc 1, và khi l=1, số
lượng tử m có thể là –1,0,+1. Trong mỗi trường
hợp, spin của electron có thể là +1/2 hoặc –1/2. Do
đó, đối với n=2 có 8 trạng thái lượng tử
khả dĩ. Neon có 10 electron. Hai electron ở mức n=1 và 8
electron ở mức n=2. Bây giờ mức năng lượng
thứ hai đầy, có nghĩa là Neon cũng là nguyên tử
khí trơ.
Từ nghiệm của phương trình sóng
schrodinger cho nguyên tử một
electron, cộng với khái niệm về spin của electron
và nguyên lí loại trừ Pauli, chúng ta có thể xây dựng
nên bảng tuần hoàn các nguyên tố. Khi số nguyên tử
của nguyên tố tăng, những electron sẽ bắt
đầu tương tác với nhau vì thế việc xây dựng
bảng tuần hoàn sẽ hơi khác chút ít so với
phương pháp trình bày ở đây.
Video sau đây sẽ
mô tả sự phân bố electron vào các mức năng lượng: