2.3|ỨNG
DỤNG CỦA PHƯƠNG TRÌNH SÓNG SCHRODINGER
Bây giờ chúng ta
sẽ áp dụng phương trình sóng Schrodinger cho một số
bài toán cụ thể với các hàm thế khác nhau. Những
trường hợp này sẽ minh họa các phương
pháp được dùng để giải phương trình Schrodinger
và kết quả của những trường hợp này sẽ
cung cấp cho chúng ta kiến thức về hành vi của
electron trong các thế năng khác nhau. Chúng ta sẽ dùng những
kết quả được rút ra để thảo luận
về tính chất của bán dẫn.
2.3.1
Electron trong không gian tự do
Đầu tiên,
xét chuyển động của một electron trong không gian
tự do. Nếu không có lực tác động lên hạt thì
hàm thế V(x) sẽ bằng
0. Do đó, từ phương trình (2.13) phương trình
sóng không phụ thuộc thời gian có thể được
viết là
![]() (2.19)
(2.19)
Nghiệm của
phương trình vi phân này có thể được viết
dưới dạng
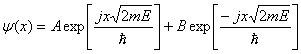 (2.20)
(2.20)
Phần phụ thuộc thời gian của
nghiệm vẫn sẽ là
![]() (2.21)
(2.21)
Do đó, nghiệm
toàn phần của hàm sóng là
![]() (2.22)
(2.22)
Đây là nghiệm
sóng chạy, điều đó có nghĩa là hạt di chuyển
trong không gian tự do được biễu diễn bằng
sóng chạy. Số hạng đầu tiên, với hệ số
A là sóng chạy theo hướng +x,
còn số hạng thứ hai với hệ số B là sóng chạy
theo hướng –x. Giá trị
của những hệ số này sẽ được xác
định từ điều kiện biên. Chúng ta sẽ gặp
lại nghiệm sóng chạy của electron trong tinh thể
hoặc vật liệu bán dẫn.
Giả sử rằng chúng ta có một hạt
di chuyển theo hướng +x,
nó sẽ được mô tả bởi sóng chạy +x, hệ số B=0. Chúng ta có thể viết
nghiệm sóng chạy dưới dạng
Ψ(x,t)=Aexp[j(kx–ωt)]
(2.23)
ở đây k là số sóng và
![]() (2.24)
(2.24)
λ là bước
sóng, so sánh phương trình (2.22) với phương trình (2.23)
suy ra bước sóng sẽ là
![]() (2.25)
(2.25)
Từ nguyên lí
lưỡng tính sóng hạt De Broglie, bước sóng cũng
có thể được viết là
![]() (2.26)
(2.26)
Một hạt tự
do với năng lượng xác định cũng sẽ
có bước sóng và động lượng xác định.
Hàm mật độ xác suất ψ(x,t)ψ*(x,t)=AA*, là hằng
số không phụ thuộc vị trí. Hạt tự do với
động lượng xác định có thể được
tìm thấy với xác suất bằng nhau ở mọi
nơi. Kết quả này phù hợp với nguyên lí bất
định Heisenberg: động lượng sẽ dẫn
đến vị trí không xác định.
 Một hạt tự do định
xứ được xem như bó sóng (được hình
thành bằng cách chồng chất nhiều hàm sóng với
động lượng khác nhau). Chúng ta sẽ không xem xét bó
sóng ở đây.
Một hạt tự do định
xứ được xem như bó sóng (được hình
thành bằng cách chồng chất nhiều hàm sóng với
động lượng khác nhau). Chúng ta sẽ không xem xét bó
sóng ở đây.
2.3.2
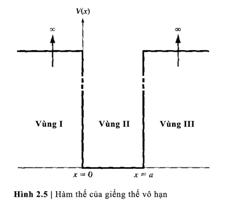
Giếng thế vô hạn
Bài toán hạt chuyển
động trong giếng thế vô hạn là ví dụ điễn
hình về hạt liên kết. Thế V(x) là hàm theo tọa độ được biễu
diễn trong hình 2.5. Hạt được giả sử tồn
tại trong vùng II, cũng có nghĩa là nó bị giam trong vùng
không gian xác định.
Từ
phương trình (2.13) suy ra phương trình sóng Schrodinger
độc lập thời gian trong trường hợp này
là
![]() (2.13)
(2.13)
ở đây E là năng lượng toàn phần
của hạt. Nếu E xác
định, hàm sóng phải bằng 0 cả trong vùng I và III.
Hạt không thể xuyên qua hàng rào thế xác định này,
vì vậy xác suất tìm thấy hạt trong vùng I và vùng III bằng
0
Phương trình sóng Schrodinger độc lập
thời gian trong vùng II, ở đây V=0 là
![]() (2.27)
(2.27)
Nghiệm của
phương trình này có dạng
![]() (2.28)
(2.28)
ở đây
![]() (2.29)
(2.29)
Điều kiện biên liên tục của
hàm sóng cho ta
Ψ(x=0)=ψ(x=a)=0 (2.30)
Áp dụng điều
điều kiện biên tại x=0,
chúng ta có A1 phải
bằng 0. Tại x=a, chúng ta
có
Ψ(x=a)=0=A2sinKa (2.31)
Phương trình
này có nghĩa nếu Ka=nπ,
ở đây n là số nguyên dương n=1,2,3,…. được gọi là số lượng
tử. Chúng ta có thể viết
![]() (2.32)
(2.32)
Giá trị âm của
n sẽ làm cho hàm sóng có dấu âm và tương ứng với
các hàm mật độ xác suất giống với trường
hợp n dương. Về mặt vật lí, chúng ta không thể
phân biệt bất cứ sự khác nhau nào giữa các nghiệm
+n và –n. Bởi vì sự dư thừa này, những giá
trị âm của n sẽ
không được xét đến.
Hệ số A2 có thể tìm
được bằng cách dùng điều kiện biên chuẩn
hóa được cho trong phương trình (2.18) là 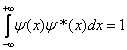 . Vì hàm sóng là hàm thực nên ψ(x)=ψ*(x). Thế hàm sóng
vào phương trình (2.18) chúng ta có
. Vì hàm sóng là hàm thực nên ψ(x)=ψ*(x). Thế hàm sóng
vào phương trình (2.18) chúng ta có
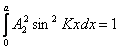 (2.33)
(2.33)
Tính tích phân sau
đó ta suy ra được
![]() (2.34)
(2.34)
Cuối cùng nghiệm độc lập thời
gian là
![]() ở đây n=1,2,3…………. (2.35)
ở đây n=1,2,3…………. (2.35)
Nghiệm này biễu diễn electron trong giếng
thế không xác định và là nghiệm sóng dừng.
Electron tự do được biễu diễn bởi sóng
chạy, và bây giờ hạt liên kết được biễu
diễn bằng sóng dừng.
Tham số K trong nghiệm được
định nghĩa bởi phương trình (2.29) và (2.32). Từ
hai biểu thức này của K, suy ra
![]() (2.36)
(2.36)
Do đó năng
lượng toàn phần là
![]() ở
đây n=1, 2, 3…………
(2.37)
ở
đây n=1, 2, 3…………
(2.37)
Đối với hạt trong giếng thế
vô hạn, hàm sóng là
![]() (2.38)
(2.38)
Ở đây hằng
số K phải có những giá trị rời rạc,
nghĩa là năng lượng toàn phần của hạt chỉ
có những giá trị rời rạc. Kết quả này có
nghĩa là năng lượng của hạt bị lượng
tử hóa. Nghĩa là, năng lượng của hạt chỉ
có những giá trị rời rạc nào đó. Sự lượng
tử hóa năng lượng của hạt trái ngược
với những kết quả của vật lí cổ
điển. Vật lí cổ điển chỉ cho phép hạt
có những giá trị năng lượng liên tục.
Năng lượng rời rạc dẫn đến những
trạng thái lượng tử sẽ được xét
chi tiết hơn trong chương này và những
chương sau. Sự lượng tử hóa năng lượng
của hạt liên kết là kết quả cực kì quan trọng.
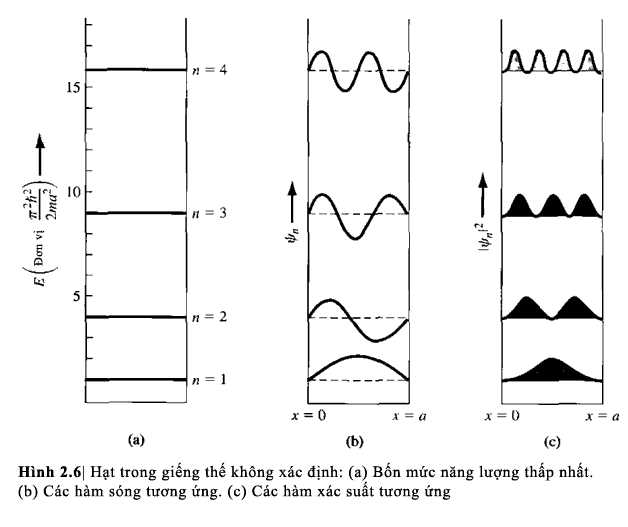
Hình 2.6a biễu diễn 4 mức năng
lượng đầu tiên của hạt trong giếng thế
không xác định, và hình 2.6b và 2.6c biễu diễn hàm sóng
và hàm xác suất tương ứng. Chúng ta có thể rút ra rằng
khi năng lượng tăng, xác suất tìm thấy hạt
tại vị trí x bất kì
cũng trở nên đồng đều hơn.
2.3.3
Hàm thế bậc thang
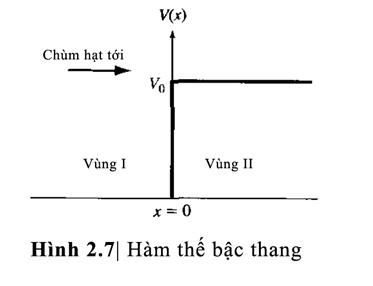
Bây giờ xét hàm
thế bậc thang được biễu diễn trong hình
2.7. Trong phần trước, chúng ta đã xét một hạt
bị giam giữa hai hàng rào thế. Trong ví dụ này, chúng
ta sẽ giả sử rằng có một dòng hạt xuất
phát từ –∞ và chuyển động theo hướng +x . Kết quả đáng chú ý
thu được trong trường hợp năng lượng
toàn phần của hạt nhỏ hơn độ cao hàng
rào, hoặc E<V0.
Một lần nửa chúng ta cần xét
phương trình sóng không phụ thuộc thời gian trong mỗi
vùng. Trong vùng I, V=0,
phương trình sóng là
![]() (2.39)
(2.39)
Nghiệm tổng
quát của phương trình này có thể viết dưới
dạng
![]() (x≤0)
(2.40)
(x≤0)
(2.40)
ở đây, hằng
số K1 là
![]() (2.41)
(2.41)
Số hạng thứ
I trong phương trình (2.40) là sóng chạy theo hướng +x biễu diễn sóng tới,
và số hạng thứ 2 là sóng chạy tho hướng –x biễu diễn sóng phản
xạ. Như trong trường hợp của hạt tự
do, những hạt tới và hạt phản xạ
được biễu diễn bằng sóng chạy.
Đối với sóng tới, A1A1*
là hàm mật độ xác suất của những hạt tới.
Nếu chúng ta nhân hàm mật độ xác suất này với
vận tốc tới thì υi.A1.A1*
là thông lượng hạt tới (đơn vị là #/cm2-s). Tương tự,
đại lượng υr.B1.B1*
là thông lượng hạt phản xạ, ở đây
υr là vận tốc của sóng phản xạ
(υi và υr trong những số hạng
này chỉ là giá trị độ lớn của vận tốc)
Trong vùng II, thế năng V=V0. Nếu chúng ta giả sử rằng
E<V0 thì phương trình vi phân mô tả hàm sóng
trong vùng II có thể được viết là
![]() (2.42)
(2.42)
Nghiệm tổng
quát có thể được viết dưới dạng
![]() (x≥0)
(2.43)
(x≥0)
(2.43)
ở đây ![]() (2.44)
(2.44)
Hàm sóng ψ2 phải xác định khi
x≥0. Điều đó cũng có nghĩa là cho dù x tiến
đến vô cùng thì ψ2 cũng phải xác định.
Nhưng khi thế x=∞ vào biểu thức của ψ2
trong (2.43) thì số hạng thứ hai sẽ bằng vô
cùng, dẫn đến cả hàm sóng cũng bằng vô cùng.
Muốn điều này không xảy ra thì hệ số B2 phải bằng 0.
Hàm sóng lúc này được viết là
![]() (2.45)
(2.45)
Hàm sóng tại x=0 phải liên tục:
ψ1(0)=ψ2(0) (2.46)
Do đó từ
phương trình (2.40), (2.45) và (2.46), chúng ta thu được
A1+B1=A2 (2.47)
Bởi vì hàm thế xác định ở mọi
nơi, đạo hàm bậc I của hàm sóng phải liên tục:
![]() (2.48)
(2.48)
Dùng phương
trình (2.40), (2.45) và (2.48), chúng ta thu được
jK1A1–jK1B1=–K2A2
(2.49)
Chúng ta có thể
giải phương trình (2.47) và (2.49) để xác định
hệ số B1 và A2 theo hệ số
sóng tới A1. Kết quả là
![]() (2.50a)
(2.50a)
Và
![]() (2.50b)
(2.50b)
Hàm mật độ
xác suất phản xạ là
![]() (2.51)
(2.51)
Chúng ta có thể định nghĩa hệ số
phản xạ R là tỉ số của thông lượng phản
xạ và thông lượng tới
![]() (2.52)
(2.52)
ở đây υi
và υr tương ứng là vận tốc tới
và vận tốc phản xạ của hạt. Trong vùng I, V=0 vì thế E=T, ở đây T là động năng của hạt.
Động năng được viết là:
T=(1/2)mυ2
(2.53)
Vì thế, từ
phương trình (2.41) hằng số K1 có thể
được viết là
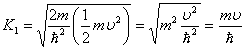 (2.54)
(2.54)
Do đó, vận tốc
tới có thể được viết là
![]() (2.55)
(2.55)
Bởi
vì hạt phản xạ cũng tồn tại trong vùng I,
độ lớn của vận tốc phản xạ là
![]() (2.56)
(2.56)
Độ
lớn của vận tốc tới và vận tốc phản
xạ bằng nhau. Do đó, hệ số phản xạ là
![]() (2.57)
(2.57)
Thế
những biểu thức từ phương trình (2.51) vào
phương trình (2.57),chúng ta thu được
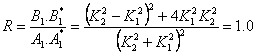 (2.58)
(2.58)
Kết
quả R=1 có nghĩa là tất cả những hạt đến
hàng rào thế có năng lượng E<V0 cuối cùng đều bị phản
xạ. Chúng không được hấp thụ hoặc truyền
qua hàng rào thế. Kết quả này hoàn toàn phù hợp với
cơ học cổ điển và chúng ta tự hỏi rằng
tại sao phải xét vấn đề này theo cơ học
lượng tử. Kết quả đáng quan tâm xuất hiện
tại vùng II.
Nghiệm trong vùng II
được cho bởi phương trình (2.45) là ![]() . Hệ số A2
theo phương trình (2.47) là A2=A1+B1,
hệ thức này được chúng ta rút ra từ điều
kiện biên. Đối với trường hợp E<V0, hệ số A2 khác 0. Nếu A2 khác 0 thì hàm mật
độ xác suất ψ2(x).ψ2(x)*
của hạt trong vùng II khác 0. Kết quả này chứng tỏ
rằng có một xác suất nào đó để chùm hạt
tới xuyên qua hàng rào và tồn tại ở vùng II. Xác suất
để hạt xuyên qua hàng rào thế là sự khác nhau
cơ bản giữa cơ học cổ điển và
cơ học lượng tử: sự xuyên hầm là không
được phép theo quan điểm cổ điển. Mặc
dù có xác suất để hạt chui qua hàng rào , nhưng hệ
số phản xạ trong vùng I bằng 1, cuối cùng hạt
trong vùng II sẽ chuyển động lòng vòng và sau đó
quay trở về vùng I.
. Hệ số A2
theo phương trình (2.47) là A2=A1+B1,
hệ thức này được chúng ta rút ra từ điều
kiện biên. Đối với trường hợp E<V0, hệ số A2 khác 0. Nếu A2 khác 0 thì hàm mật
độ xác suất ψ2(x).ψ2(x)*
của hạt trong vùng II khác 0. Kết quả này chứng tỏ
rằng có một xác suất nào đó để chùm hạt
tới xuyên qua hàng rào và tồn tại ở vùng II. Xác suất
để hạt xuyên qua hàng rào thế là sự khác nhau
cơ bản giữa cơ học cổ điển và
cơ học lượng tử: sự xuyên hầm là không
được phép theo quan điểm cổ điển. Mặc
dù có xác suất để hạt chui qua hàng rào , nhưng hệ
số phản xạ trong vùng I bằng 1, cuối cùng hạt
trong vùng II sẽ chuyển động lòng vòng và sau đó
quay trở về vùng I.
2.3.4 Hàng rào thế
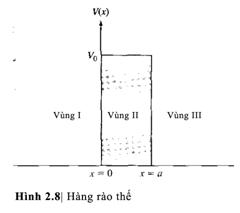 Xét
hàng rào thế được biễu diễn trong hình 2.8. Một
lần nữa, vấn đề đáng quan tâm hơn là
trường hợp năng lượng toàn phần của
hạt tới E<V0.
Chúng ta lại giả sử rằng chúng ta có một dòng các
hạt tới xuất phát từ miềm âm của trục
x và di chuyển theo hướng +x. Như trước, chúng
ta cần giải phương trình sóng Schrodinger độc
lập thời gian trong 3 vùng. Nghiệm của phương
trình sóng trong vùng I, II và III tương ứng là:
Xét
hàng rào thế được biễu diễn trong hình 2.8. Một
lần nữa, vấn đề đáng quan tâm hơn là
trường hợp năng lượng toàn phần của
hạt tới E<V0.
Chúng ta lại giả sử rằng chúng ta có một dòng các
hạt tới xuất phát từ miềm âm của trục
x và di chuyển theo hướng +x. Như trước, chúng
ta cần giải phương trình sóng Schrodinger độc
lập thời gian trong 3 vùng. Nghiệm của phương
trình sóng trong vùng I, II và III tương ứng là:
![]() (2.59a)
(2.59a)
![]() (2.59b)
(2.59b)
![]() (2.59c)
(2.59c)
Ở đây
![]() (2.60a)
(2.60a)
Và
![]() (2.60b)
(2.60b)
Hệ số B3
trong phương trình (2.59c) biễu diễn sóng chạy âm
trong vùng III. Tuy nhiên, khi một hạt đi vào trong vùng III,
không có sự thay đổi thế năng để gây ra
phản xạ; do đó, hệ số B3 phải bằng
0. Chúng ta phải giữ cả những số hạng
lũy thừa trong phương trình (2.59b) bởi vì độ
rộng hàng rào thế xác định; nghĩa là không số
hạng nào trở thành không liên kết. Chúng ta có 4 điều
kiện biên tại x=0 và x=a tương ứng với những
hàm sóng và đạo hàm bậc nhất của nó phải
liên tục. Chúng ta có thể tìm các hệ số B1,
A2, B2 và B3 theo A1. Nghiệm trong
ba vùng được biễu diễn trong hình 2.9.
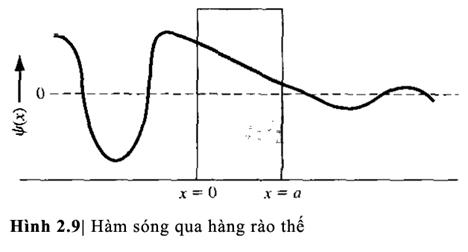
Một thông số đáng quan tâm là hệ số
truyền qua được định nghĩa là tỉ số
giữa thông lượng được truyền qua trong
vùng III với thông lượng tới trong vùng I. Do đó, hệ
số truyền qua T là:
![]() (2.61)
(2.61)
ở đây υt
và υi là vận tốc của những hạt
truyền qua và những hạt tới. Bởi vì thế
năng V=0 ở cả vùng I
và vùng III nên vận tốc tới và vận tốc truyền
qua bằng nhau. Hệ số truyền qua có thể
được xác định bằng cách cách giải những
phương trình điều kiện biên. Đối với
trường hợp đặc biệt khi E<<V0, chúng ta tìm được:
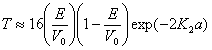 (2.62)
(2.62)
Phương trình (2.62) có nghĩa là có một
xác suất nào đó để một hạt xuyên qua hàng rào
thế và đi vào trong vùng III. Hiện tượng này
được gọi là sự chui hầm và quá mâu thuẫn
với cơ học cổ điển. Sau này chúng ta sẽ
thấy hiện tương chui hầm lượng tử
này sẽ được áp dụng trong vật lí bán dẫn
như thế nào, chẳng hạn như diode chui hầm.
Những ứng dụng của phương
trình sóng Schrodinger với những hàm thế năng một
chiều khác nhau được tìm thấy trong các bài tập
cuối chương. Một trong số các hàm thế này biễu
diễn cấu trúc giếng lượng tử trong các thiết
bị bán dẫn hiện đại.