2.2 PHƯƠNG TRÌNH SÓNG
SCHRODINGER
Những
kết quả thực nghiệm trên sóng điện từ
và hạt vi mô không thể giải thích được bằng
các định luật cơ học cổ điển,
điều đó đòi hỏi phải xây dựng một
môn cơ học mới cho các hạt vi mô. Năm 1926,
Schrodinger đã xây dựng cơ học sóng, nó hợp nhất
nguyên lí lượng tử do Planck đưa ra và nguyên lí
lưỡng tính sóng hạt của De Broglie. Dựa trên
nguyên lí lưỡng tính sóng hạt, chúng ta sẽ mô tả
chuyển động của electron trong tinh thể bằng
lí thuyết sóng. Lí thuyết sóng này được mô tả
bởi phương trình sóng Schrodinger.
2.2.1 Phương trình sóng
Phương
trình sóng Schrodinger một chiều, phi tương đối
tính là:
![]() (2.6)
(2.6)
ở
đây ψ(x,t) là hàm sóng, V(x) là thế năng được giả sử
là không phụ thuộc thời gian, m là khối lượng của hạt và j là một hằng số ảo
bằng ![]() . Có một luận cứ lí thuyết
để dẫn ra phương trình sóng Schrodinger, nhưng
phương trình là một định đề cơ bản
của cơ học lượng tử. Hàm sóng ψ(x,t) sẽ được
dùng để mô tả hành vi của hệ và về mặt
toán học ψ(x,t) là một
hàm phức.
. Có một luận cứ lí thuyết
để dẫn ra phương trình sóng Schrodinger, nhưng
phương trình là một định đề cơ bản
của cơ học lượng tử. Hàm sóng ψ(x,t) sẽ được
dùng để mô tả hành vi của hệ và về mặt
toán học ψ(x,t) là một
hàm phức.
Chúng ta có thể xác định
phần phụ thuộc thời gian của hàm sóng và phần
phụ thuộc tọa độ bằng cách dùng kĩ thuật
tách biến. Giả sử rằng hàm sóng có thể
được viết dưới dạng
![]() (2.7)
(2.7)
ở
đây ψ(x) là hàm theo tọa
độ x và ![]() là hàm theo thời
gian. Thế dạng này của nghiệm vào phương
trình sóng Schrodinger, chúng ta thu được:
là hàm theo thời
gian. Thế dạng này của nghiệm vào phương
trình sóng Schrodinger, chúng ta thu được:
![]() (2.8)
(2.8)
Nếu
chia cho hàm sóng toàn phần, phương trình 2.8 trở thành
![]() (2.9)
(2.9)
Bởi
vì vế trái của phương trình là hàm theo vị trí x và
vế phải của phương trình là hàm theo thời
gian, muốn phương trình này có nghĩa thì mỗi vế
của phương trình này phải bằng hằng số.
Chúng ta kí hiệu hằng số này là η.
Do
đó, phần phụ thuộc thời gian của
phương trình (2.9) được viết là
![]() (2.10)
(2.10)
Nghiệm
của phương trình 2.10 có thể được viết
dưới dạng
![]() (2.11)
(2.11)
Dạng
nghiệm này là dạng hàm mũ của sóng sin, ở đây
η/ћ là tần số
bức xạ ω. Chúng ta có ![]() hoặc
E=hω/2π. Do đó, ω=η/ћ =E/ћ vì thế hằng
số tách biến η bằng năng lượng E của
hạt.
hoặc
E=hω/2π. Do đó, ω=η/ћ =E/ћ vì thế hằng
số tách biến η bằng năng lượng E của
hạt.
Phần không phụ thuộc
thời gian của phương trình sóng Schrodinger bây giờ
có thể được viết từ phương trình
(2.9) là:
![]() (2.12)
(2.12)
ở
đây hằng số tách biến là năng lượng toàn
phần E của hạt. Phương trình (2.12) có thể
được viết là:
![]() (2.13)
(2.13)
ở
đây m là khối lượng của hạt, V(x) là thế năng của hạt,
và E là năng lượng
toàn phần của hạt. Phương trình sóng Schrodinger
không phụ thuộc thời gian cũng có thể được
dẫn ra dựa vào phương trình sóng cổ điển
như được chứng minh trong phần phụ lục
E. Cách tiếp cận này đơn giản nhưng nó chứng
tỏ sự đáng tin cậy của phương trình sóng
Schrodinger độc lập thời gian.
2.2.2 Ý nghĩa vật lí của
hàm sóng
Mục
đích cuối cùng của chúng ta là dùng phương trình
sóng ψ(x,t) để mô tả hành vi của
electron trong tinh thể. Hàm ψ(x,t)
là hàm sóng, vì vậy cần phải biết mối quan hệ
giữa hàm và electron là gì. Hàm sóng toàn phần là tích của
hàm sóng không phụ thuộc thời gian và hàm sóng phụ thuộc
thời gian. Từ (2.7) chúng ta có
![]() (2.14)
(2.14)
Bởi
vì hàm sóng toàn phần là hàm phức nên bản thân nó không thể
biễu diễn một đại
lượng vật lí thực.
Năm 1926, Max Born đã phát
biểu rằng bình phương modun hàm sóng |ψ(x,t)|2 dx
là xác suất tìm thấy hạt trong khoảng từ x đến x+dx tại một thời điểm nào đó, hoặc
|ψ(x,t)|2 là hàm mật
độ xác suất. Chúng ta có:
![]() (2.15)
(2.15)
Ở
đây ψ*(x,t) là hàm liên hợp
phức. Do đó
![]()
Vì
thế tích của hàm sóng toàn phần và liên hợp phức
của nó sẽ bằng
![]() (2.16)
(2.16)
Do
đó, chúng ta có
![]() (2.17)
(2.17)
Là
hàm mật độ xác suất và không phụ thuộc thời
gian. Một sự khác biệt lớn giữa cơ học
cổ điển và cơ học lượng tử là
trong cơ học cổ điển, vị trí của hạt
có thể được xác định chính xác, trong khi
đó trong cơ học lượng tử, vị trí của
hạt được xác định theo xác suất. Chúng
ta sẽ xác định hàm mật độ xác suất
trong vài trường hợp, và bởi vì nó không phụ thuộc
thời gian, nói chung, chúng ta sẽ chỉ quan tâm đến
những phương trình sóng không phụ thuộc thời
gian.
2.2.3 Điều kiện
biên
Bởi
vì hàm sóng |ψ(x,t)|2
biễu diễn hàm mật độ xác suất, do đó,
đối với một hạt, chúng ta phải có
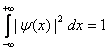 (2.18)
(2.18)
Xác
suất tìm thấy hạt trong toàn không gian là tất nhiên.
Phương trình (2.18) cho phép chúng ta chuẩn hóa hàm sóng và là
điều kiện được dùng để xác định
những hệ số trong hàm sóng.
Điều kiện còn lại
áp đặt cho hàm sóng và đạo hàm của nó. Tuy nhiên
chúng ta phải phát biểu điều kiện biên và
đưa ra lí lẽ biện minh tại sao chúng ta phải
áp đặt những điều kiện ấy. Hàm sóng và
đạo hàm bậc nhất của nó phải có tính chất
sau nếu năng lượng toàn phần E và thế năng V(x)
của nó xác định ở mọi nơi.
Điều kiện 1: ψ(x) phải xác định,
liên tục và đơn trị.
Điều kiện 2: ![]() phải xác
định, liên tục và đơn trị.
phải xác
định, liên tục và đơn trị.
Bởi vì |ψ(x)|2 là mật độ xác suất
nên ψ(x) phải xác định
và đơn trị. Nếu mật độ xác suất
không xác định tại điểm nào đó trong không
gian thì xác suất tìm thấy hạt tại vị trí này sẽ
là chắc chắn (100%) và nguyên lí bất định sẽ
bị vi phạm. Nếu năng lượng toàn phần E và thế năng V(x) xác định ở mọi
nơi thì từ phương trình (2.13), đạo hàm bậc
II phải xác định, nghĩa là đạo hàm bậc I
phải liên tục. Đạo hàm bậc I có liên quan đến
động lượng hạt, là đại lượng
xác định và đơn trị. Cuối cùng, đạo
hàm bậc I xác định có nghĩa là chính hàm số đó
phải liên tục. Trong một vài trường hợp
đặc biệt mà chúng ta sẽ xem xét, hàm thế sẽ
không xác định tại một vùng nào đó của không
gian. Đối với trường hợp này, đạo
hàm bậc nhất không liên tục,
nhưng điều kiện biên còn lại vẫn còn
đúng.