CHƯƠNG
II
Cơ Bản Về Cơ Học Lượng Tử
TỔNG QUAN
Mục
đích của tài liệu này là giúp người đọc hiểu về hoạt động và đặc tính của thiết
bị bán dẫn. Một cách lí tưởng, chúng ta sẽ khảo sát những thiết bị này ngay tức
khắc. Tuy nhiên, để hiểu đặc tuyến V-A, chúng ta cần hiểu biết về đặc tính chuyển
động của electron trong tinh thể khi electron chịu sự tác động của các thế năng
khác nhau.
Chuyển động của các vật thể vĩ mô, chẳng
hạn như các hành tinh và vệ tinh có thể được tiên đoán với độ chính xác cao
dùng vật lí cổ điển dựa trên các định luật chuyển động của Newton. Trong khi đó
những thực nghiệm với electron và sóng điện từ tần số cao dẫn đến những kết quả
mâu thuẫn với vật lí cổ điển. Tuy nhiên, những kết quả thực nghiệm này có thể
được tiên đoán bằng các định luật cơ học lượng tử. Lí thuyết sóng cơ học lượng
tử là cơ sở cho lí thuyết vật lí bán dẫn.
Chúng ta sẽ tập trung vào những vật liệu
bán dẫn mà tính chất điện của nó liên quan trực tiếp đến đặc tính chuyển động của
electron trong mạng tinh thể. Hành vi và đặc tính của những electron này có thể
được mô tả bằng cơ học sóng. Cơ học sóng sử dụng phương trình Schrodinger và
phương trình này được giới thiệu trong chương này.
Mục tiêu của chương này là giới thiệu vắn tắt về cơ học lượng tử để cho người đọc thu được kiến thức và dần
dần quen với phương pháp phân tích. Những kiến thức nhập môn này hình thành nên
cơ sở của vật lí bán dẫn.
2.1|NHỮNG NGUYÊN LÍ CỦA CƠ HỌC LƯỢNG
TỬ
Trước
khi nghiên cứu về cơ sở toán học của cơ học lượng tử, có ba nguyên lí mà chúng
ta cần xem xét: nguyên lí lượng tử hóa năng lượng, nguyên lí lưỡng tính sóng-hạt
và nguyên lí bất định.
2.1.1 Lượng tử hóa năng lượng
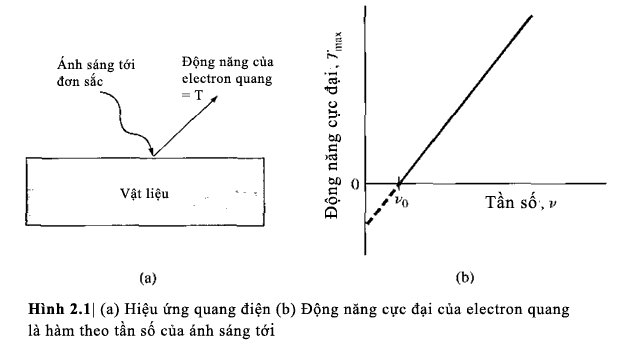
Một thí nghiệm chứng tỏ có sự mâu thuẫn
giữa kết quả thực nghiệm với lí thuyết cổ điển của ánh sáng là hiệu ứng quang
điện. Nếu ánh sáng không đơn sắc được chiếu đến bề mặt sạch của vật liệu,
thì những electron (những electron quang)
có thể được phát ra từ bề mặt. Theo vật lí cổ điển, nếu cường độ ánh sáng đủ lớn,
động năng của electron sẽ lớn hơn công thoát và electron sẽ thoát ra khỏi bề mặt
kim loại không phụ thuộc vào tần số của ánh sáng tới. Điều này thực tế không xảy
ra. Hiệu ứng quan sát được trong thực tế là, với cường độ ánh sáng tới không đổi,
nếu tần số ánh sáng nhỏ hơn một tần số υ0 nào đó (υ0 là tần
số giới hạn phụ thuộc vào loại vật liệu cụ thể) thì sẽ không có electron nào được
thoát ra từ bề mặt vật liệu. Còn khi υ ≥ υ0 động năng cực đại của
electron quang biến đổi tuyến tính theo tần số. Kết quả này được biễu diễn
trong hình 2.1. Nếu cường độ ánh sáng tới biến đổi còn tần số không đổi, tốc độ
phát xạ electron quang thay đổi, nhưng động năng cực đại vẫn giữ nguyên.
Tiếp
theo, chúng ta sẽ thực hiện một thí nghiệm ảo về hiệu ứng quang điện. Trước tiên,
hãy xem hình vẽ mô tả các bộ phận và cách điều khiển thí nghiệm.
Nhấp vào đây để thực hiện thí nghiệm.
Vào năm 1900, Planck đã giả thuyết rằng
bức xạ nhiệt được phát ra từ bề mặt đun nóng thành những lượng năng lượng nhỏ rời
rạc được gọi là lượng tử. Năng lượng của những lượng tử này là E=hυ, ở đây υ là
tần số của bức xạ và h được gọi là hằng số Planck (h=6,625.10–34
J-s). Sau đó vào năm 1905, Einstein đã giải thích hiệu ứng quang điện bằng cách
giả thiết rằng năng lượng trong sóng ánh sáng bao gồm những lượng nhỏ rời rạc.
Những lượng nhỏ rời rạc này được gọi là photon có năng lượng là E=hυ. Do đó, một
photon với năng lượng đủ lớn mới có thể va chạm vào electron ở bề mặt vật liệu.
Năng lượng nhỏ nhất để bứt electron ra khỏi bề mặt được gọi là công thoát của vật
liệu.
Và phần năng lượng dư sẽ biến thành động
năng của electron quang. Kết quả này đã được xác nhận bằng thực nghiệm và được
minh họa trong hình 2.1. Hiệu ứng quang điện chứng tỏ bản chất gián đoạn của
photon và chứng minh hành vi giống hạt của photon.
Động năng cực đại của electron quang có
thể viết là
(2.1)
ở
đây 
là năng lượng
photon tới và 
là năng lượng cực tiểu, hoặc công thoát cần để bứt
electron ra khỏi bề mặt.
2.1.2 Lưỡng tính sóng-hạt
Chúng ta dã thấy trong phần trước rằng
trong hiệu ứng quang điện, sóng ánh sáng hành xử như thể chúng là hạt. Hành vi
giống như hạt của sóng điện từ cũng là công cụ để giải thích hiệu ứng Compton.
Trong thí nghiệm này, chùm tia X được chiếu tới chất rắn. Một phần của chùm tia
X bị lệch và tần số của sóng lệch này thay đổi so với sóng tới. Nếu chúng ta
xét bài toán này như sự va chạm giữa các photon tia X và các electron trong chất
rắn, sử dụng định luật bảo toàn năng lượng và động lượng, chúng ta có thể suy
ra được kết quả hoàn toàn phù hợp với thực
Năm 1924, de Broglie đã giả thuyết về sự
tồn tại của sóng vật chất. Ông ta lập luận rằng sóng biểu hiện hành vi giống như hạt, vì thế có thể
tiên đoán rằng hạt cũng sẽ biểu hiện những tính chất giống như sóng. Đây là giả
thuyết De Broglie về sự tồn tại của lưỡng tính sóng hạt. Động lượng của photon
là:
p=h/λ
(2.2)
ở
đây λ là bước sóng của sóng ánh sáng. Do đó, De Broglie đã giả thuyết rằng bước
sóng của hạt có thể được biểu diễn là
λ=h/p
(2.3)
ở
đây p là động lượng của hạt và λ được
gọi là bước sóng De Broglie của sóng vật chất.
Bản chất sóng của electron đã được kiểm
tra theo vài cách. Như chúng ta đã biết,
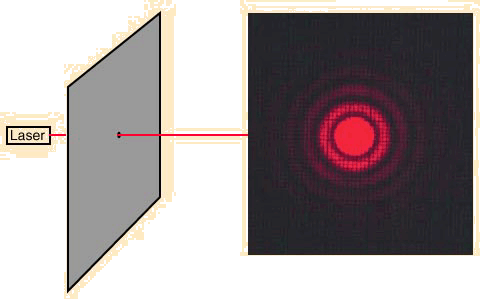
sóng được đặc trưng bởi các hiện tượng giao thoa và nhiễu xạ. Nhiễu xạ là hiện
tượng ánh sáng sau khi đi qua những khe hẹp có độ lớn cỡ bước sóng của chính
ánh sáng đó thì các tia sáng không còn truyền thẳng. Về mặt thực nghiệm, chúng
ta sẽ thấy trên màn quan sát xuất hiện những vân sáng tối xen kẽ nhau với cường
độ khác nhau. Chẳng hạn khi ánh sáng laser (là ánh sáng đơn sắc) đi qua một lỗ
nhỏ hình cầu có đường kính xấp xỉ bằng bước sóng của nó thì trên màn quan sát
chúng ta sẽ thấy như sau:
Vì
thế, nếu muốn chứng minh electron có tính chất sóng thì chúng ta phải bố trí
thí nghiệm thế nào để cho có thể quan sát được hiện tượng nhiễu xạ electron qua
một khe nào đó. Để có hiện tượng nhiễu xạ xảy ra thì tất nhiên khe này phải có
kích thướt xấp xỉ bằng bước sóng của electron. Các khe này chính là các khe
trong mạng tinh thể của các chất rắn kết tinh.
Chẳng
hạn khi chiếu chùm electron vào tinh thể bạch kim thì chúng ta sẽ thu được một
hình ảnh như sau:
Bạn
có thấy nó cũng gồm những vân sáng và vân tối xen kẽ nhau giống như hiện tượnng
nhiễu xạ ánh sáng laser ở trên không.
Vậy là, trong thực tế có tồn tại hiện tượng
nhiễu xạ electron. Nghĩa là electron là một hạt nhưng lại thể hiện tính chất
sóng. Những dãy số như 311, 220, 111, 200 là kí hiệu các mặt mạng của tinh thể.
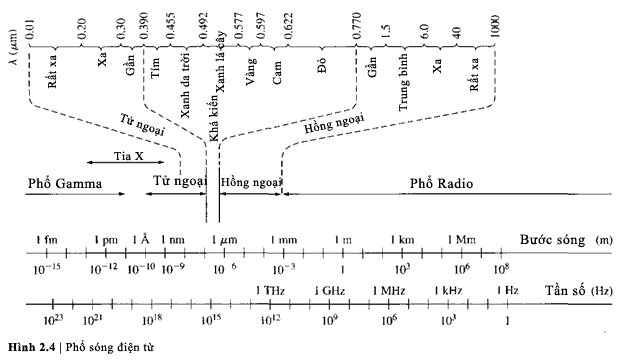
Để thu được vài đánh giá về tần số và bước
sóng liên quan đến nguyên lí lưỡng tính sóng-hạt, hình 2.4 biễu diễn thang sóng
điện từ. Chúng ta thấy rằng bước sóng 72,7 A0 thu được trong ví dụ
tiếp theo thuộc vùng tử ngoại. Thông thường, chúng ta sẽ xem xét bước sóng
trong vùng tử ngoại và nhìn thấy.
Những
bước sóng này rất ngắn so với phổ radio thông thường.
Ví dụ 2.2: Tính bước sóng de
Broglie của electron chuyển động với vận tốc 105 cm/s.
Giải
Động lượng của electron sẽ là
Do đó, bước sóng De broglie là:
Hay 
Kết luận: Kết quả này cho thấy bậc
độ lớn bước sóng De Broglie của một electron thông thường
Trong một số trường hợp sóng điện từ
hành xử như thể chúng là hạt (những photon) và thỉnh thoảng hạt hành xử như thể
chúng là sóng. Nguyên lí lưỡng tính sóng-hạt của cơ học lượng tử áp dụng chủ yếu
cho các hạt vi mô chẳng hạn như electron, nhưng cũng có thể áp dụng cho proton
và nơtron. Đối với những hạt vĩ mô, chúng ta có thể chứng tỏ rằng những phương
trình chuyển động mô tả chúng sẽ trở về những phương trình của cơ học cổ điển.
Nguyên lí lưỡng tính sóng – hạt là cơ sở để mô tả chuyển động và hành vi của
electron trong tinh thể.
Xem
phim tài liệu (tùy chọn)
2.1.3 Nguyên lí bất định
Nguyên lí bất định Heisenberg được đưa
ra vào năm 1927, cũng áp dụnh chủ yếu cho các hạt vi mô và phát biểu rằng chúng
ta không thể mô tả chính xác tuyệt đối hành vi của những hạt ở cấp độ dưới
nguyên tử này. Nguyên lí bất định mô tả mối quan hệ cơ bản giữa những biến liên
hợp, chẳng hạn như vị trí và động lượng, năng lượng và thời gian.
Phát biểu thứ nhất của nguyên lí bất định
là không thể mô tả chính xác đồng thời vị trí và động lượng của hạt. Nếu độ bất
định tọa độ là Δp và độ bất định vị
trí là Δx thì hệ thức bất định được
viết là
Δp.Δx≥ћ
(2.4)
ở
đây ћ=h/2π=1,054.10–34 J-s
và được gọi là hằng số Planck hiệu dụng. Phát biểu này có thể được khái quát
hóa cho góc và momen động lượng.
Phát biểu thứ hai của nguyên lí bất định
là không thể đồng thời mô tả chính xác tuyệt đối năng lượng và khoảng thời gian
mà hạt tồn tại ở trạng thái năng lượng này. Nếu độ bất định trong năng lượng là
ΔE và độ bất định thời gian là Δt thì hệ thức bất định được phát biểu
là
ΔE.Δt≥ћ
(2.5)
Một cách để hình dung hệ thức bất định
là xét sự đo đồng thời vị trí và động lượng, và sự đo đồng thời năng lượng và
thời gian. Hệ thức bất định muốn nói rằng những sự đo đồng thời này có độ sai lệch
trong phạm vi nào đó. Tuy nhiên, hằng số Planck hiệu dụng rất nhỏ; hệ thức bất
định chỉ có ý nghĩa cho những hạt ở cấp độ dưới nguyên tử. Và chúng ta cần nhớ
rằng hệ thức bất định là một phát biểu cơ bản và nó không liên hệ gì đến sai số
của phép đo.
Một kết quả của hệ thức bất định là
chúng ta không thể xác định chính xác vị trí của electron. Thay vào đó, chúng
ta sẽ xác định xác suất tìm thấy electron trong một khoảng nào đó. Trong chương
sau, chúng ta sẽ xây dựng hàm mật độ xác suất cho phép chúng ta xác định xác suất
mà một electron có một năng lượng nào đó. Vì vậy, trong việc mô tả hành vi của
electron, chúng ta sẽ làm việc với hàm xác suất.
Video
sau đây sẽ mô tả chuyển động của electron trong nguyên tử, bạn không thể thấy
các electron mà chỉ thấy những đám mây electron.