![]()
1.3|MẠNG
KHÔNG GIAN
Chúng ta sẽ khảo sát
đơn tinh thể với sự tuần hoàn hình học đều đặn trong sự sắp xếp nguyên tử của
nó. Một đơn vị đại diện, hoặc nhóm các nguyên tử được lặp lại sau những khoảng
đều đặn ở mỗi chiều để hình thành đơn tinh thể. Sự sắp xếp tuần hoàn của những
nguyên tử trong tinh thể được gọi là mạng.
1.3.1
Ô đơn vị và ô đơn vị tối giản
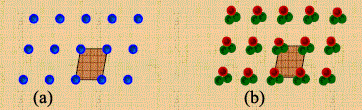
Chúng ta có thể biểu diễn
một nguyên tử (a) hoặc nhóm các nguyên tử (b) nào đó bằng một chấm được gọi là
điểm mạng. Ví dụ: trong tinh thể Silic, mỗi điểm mạng của nó là một nguyên tử
silic; còn trong tinh thể nước đá, mỗi điểm mạng của nó là phân tử nước.
Hình 1.2 biễu diễn mạng
hai chiều vô hạn bao gồm những điểm mạng. Cách đơn giản nhất để lặp lại các
nguyên tử hoặc nhóm nguyên tử là tịnh tiến. Mỗi điểm mạng trong hình 1.2 có thể
được tịnh tiến một khoảng cách na1 theo một chiều và khoảng cách mb1
theo chiều thứ 2 để tạo ra mạng 2 chiều (n, m là các số nguyên). Sự tịnh tiến
theo chiều thứ 3 sẽ tạo ra mạng 3 chiều. Những hướng tịnh tiến không cần vuông
góc nhau.
Nhìn vào hình 1.3,
chúng ta thấy rằng chỉ cần lặp lại một trong các hình bình hành A, B, C, D thì sẽ tạo ra được toàn bộ mạng tinh thể. Các
hình bình hành này gọi là các ô đơn vị. Ô đơn vị A có thể được tịnh tiến theo
hướng a2 và b2, ô đơn vị B có thể được tịnh tiến theo hướng
a3 và b3, và toàn bộ mạng 2 chiều có thể được xây dựng bằng
cách tịnh tiến cả 2 loại ô đơn vị này. Những ô đơn vị C và D trong hình 1.3
cũng có thể được dùng để xây dựng toàn bộ
mạng bằng cách dùng những phép tịnh tiến thích hợp. Vậy chúng ta có thể định
nghĩa ô đơn vị là một thể tích nhỏ của tinh thể có thể được dùng để tạo ra toàn
tinh thể. Ô đơn vị không phải là duy nhất. Những kết quả của việc khảo sát mạng
2 chiều có thể dễ dàng được mở rộng cho trường hợp 3 chiều để mô tả vật liệu
đơn tinh thể thực.
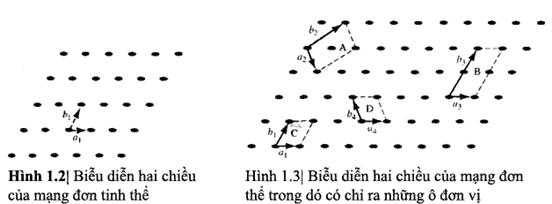
Ô đơn vị tối giản là ô đơn vị nhỏ nhất mà có thể được lặp lại để hình thành mạng.
Trong nhiều trường hợp, sẽ thuận lợi hơn nếu dùng ô đơn vị chứ không phải ô đơn
vị tối giản. Ô đơn vị được chọn có những mặt bên vuông góc trong khi những mặt
bên của ô đơn vị tối giản có thể không vuông góc.
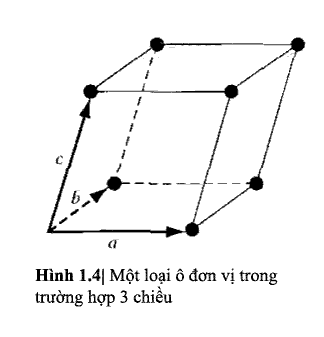 Một loại ô đơn vị 3 chiều được biễu diễn
trong hình 1.4. Mối quan hệ giữa ô này và mạng được đặc trưng bởi 3 vecto a, b,
và c. Ba vecto này không cần thiết
phải vuông góc nhau và có thể bằng nhau
hoặc không bằng nhau về độ dài. Mỗi điểm mạng trong mạng 3 chiều có thể tìm được
bằng cách dùng vecto:
Một loại ô đơn vị 3 chiều được biễu diễn
trong hình 1.4. Mối quan hệ giữa ô này và mạng được đặc trưng bởi 3 vecto a, b,
và c. Ba vecto này không cần thiết
phải vuông góc nhau và có thể bằng nhau
hoặc không bằng nhau về độ dài. Mỗi điểm mạng trong mạng 3 chiều có thể tìm được
bằng cách dùng vecto:
r = pa + qb + sc
(1.1)
ở đây p, q
và s là những số nguyên. Bởi vì vị
trí của gốc tọa độ là tùy ý, chúng ta sẽ đặt p, q và s là những số nguyên dương cho đơn giản.
1.3.2 Cấu trúc mạng cơ bản
Trước khi thảo luận về
tinh thể bán dẫn, chúng ta hãy xét 3 cấu trúc tinh thể và xác định một số tính
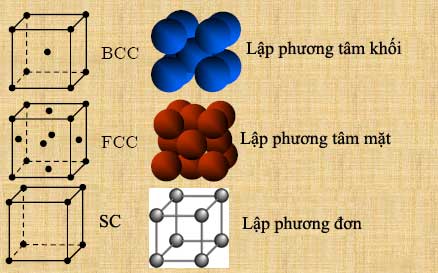
chất cơ bản của những tinh thể này. Hình 1.5 biễu diễn cấu trúc lập phương đơn,
lập phương tâm khối và lập phương tâm mặt. Đối với những cấu trúc đơn giản này,
chúng ta có thể chọn những ô đơn vị sao cho những vecto a, b, và c vuông góc với nhau và có độ dài bằng
nhau. Cấu trúc lập phương đơn (SC) có một nguyên tử đặt tại mỗi đỉnh; cấu trúc
lập phương tâm khối (BCC) có thêm một nguyên tử đặt ở tâm của hình lập phương;
và cấu trúc lập phương tâm mặt (FCC) có thêm những nguyên tử ở mỗi mặt.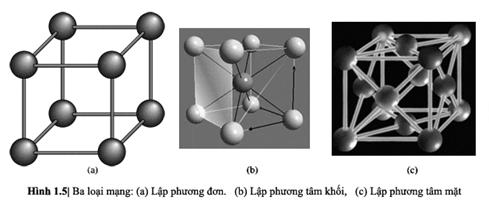
Bằng cách tìm hiểu về cấu trúc tinh thể của vật liệu và hướng mạng
của nó, chúng ta có thể xác định vài tính chất của tinh thể. Chẳng hạn, chúng
ta có thể xác định mật độ thể tích của nguyên tử.
1.3.3
Mặt phẳng tinh thể và chỉ số Miller
Bởi vì tinh thể thực có
kích thướt không xác định, nghĩa là cuối cùng chúng kết thúc tại một bề mặt.
Thiết bị bán dẫn được chế tạo ngay tại hoặc gần bề mặt vì vậy tính chất bề mặt
có thể ảnh hưởng đến đặc tính thiết bị. Chúng ta muốn mô tả những bề mặt này
theo mạng. Những bề mặt, hoặc mặt phẳng trong tinh thể có thể được mô tả bằng
cách đầu tiên xem xét giao điểm của mặt phẳng dọc theo những trục a, b, và c được
dùng để mô tả mạng.
Ví
dụ 1.2: Hãy mô tả mặt phẳng được biễu diễn trong hình 1.6. (trong hình 1.6 những điểm mạng chỉ được biễu diễn dọc
theo ba trục a, b, c)
Giải:
·
Giao
điểm của mặt phẳng với ba trục a, b, c là p=3, q=2, v s=1.
·
Lấy
nghịch đảo, chúng ta có:(1/3; 1/2; 1/1)
·
Quy
đồng mẫu số của ba phân số này: (2/6; 3/6; 6/6)
·
Những
chữ số ở tử sẽ là những chỉ số biễu diễn mặt phẳng mạng, nghĩa là chúng ta có mặt
phẳng (2,3,6). Những chữ số này cũng được gọi là chỉ số Miller.
·
Chúng
ta sẽ gọi mặt phẳng trong trường hợp tổng quát là (hkl)
·
Kết
luận: Những mặt phẳng song song với mặt phẳng trong hình 1.6 sẽ có cùng chỉ số
Miller là (2,3,6). Như vậy, các mặt phẳng song song nhau hoàn toàn tương đương
nhau.
Ba mặt phẳng thường được
xét trong tinh thể lập phương được biễu diễn trong hình 1.7. Mặt phẳng trong
hình 1.7a song song với những trục b và c vì vậy giao điểm là p=1, q=∞
và s=∞. Lấy nghịch đảo, chúng ta thu
được chỉ số Miller là (1, 0, 0), vì vậy mặt phẳng được biễu diễn trong hình
1.7a là mặt phẳng (100). Một lần nữa, bất kì mặt phẳng nào song song với mặt phẳng
được biểu diễn trong hình 1.7a 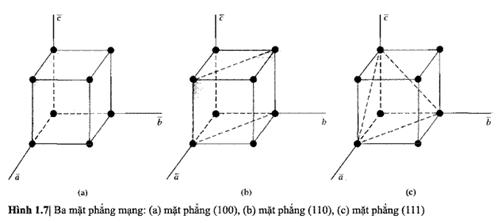
và được chia tách bằng
một số nguyên lần hằng số mạng hoàn toàn tương đương nhau và được gọi là mặt phẳng
(100). Một sự thuận lợi của việc lấy nghịch đảo giao điểm để thu được chỉ số Miller
là tránh được việc sử dụng ∞ khi mô tả mặt phẳng song song với một trục. Tuy
nhiên, nếu chúng ta mô tả mặt phẳng đi qua gốc tọa độ của hệ, chúng ta sẽ lại
thu được một hoặc một số chỉ số Miller không xác định sau khi lấy nghịch đảo của
giao điểm. Tuy nhiên, vị trí của gốc tọa độ của một hệ tọa độ là hoàn toàn tùy
ý và vì vậy bằng phép tịnh tiến gốc tọa độ đến một điểm mạng tương đương khác,
chúng ta sẽ tránh được dùng ∞ trong tập hợp những chỉ số Miller.
Đối với cấu trúc lập
phương đơn, lập phương tâm khối và lập phương tâm mặt có một bậc đối xứng cao.
Những trục có thể được quay 900 ở một trong 3 chiều và mỗi điểm mạng
lại có thể được mô tả bởi phương trình (1.1):
r=pa + qb + sc
(1.1)
Mỗi mặt của cấu trúc lập
phương được biễu diễn trong hình 1.7a hoàn toàn tương đương. Những mặt phẳng
này được nhóm với nhau và được gọi là tập những mặt phẳng {100}.
Chúng ta tiếp tục xét
những mặt phẳng được biễu diễn trong hình 1.7b và 1.7c. Giao điểm của mặt phẳng
được biễu diễn trong hình 1.7b là p=1,
q=1, và s=∞. Chỉ số Miller được tìm bằng cách lấy nghịch đảo của những giao
điểm này, và kết quả là, mặt phẳng này được gọi là mặt phẳng (110). Theo cách
tương tự, mặt phẳng được biểu diễn trong hình 1.7c được gọi là mặt phẳng (111).
Một đặc tính khác của tinh thể cũng có thể được xác định là khoảng
cách giữa những mặt phẳng tương đương gần nhất. Một đặc tính khác là mật độ bề
mặt của nguyên tử, số nguyên tử trên cm2 (#/cm2) bị cắt bởi
một mặt phẳng nào đó. Cần nhớ rằng, bán dẫn đơn tinh thể có kích thướt xác định
và phải kết thúc tại một số bề mặt. Mật độ bề mặt của nguyên tử là quan trọng
trong nhiều trường hợp, chẳng hạn trong việc xác định những vật liệu khác, như
điện môi, sẽ khớp với bề mặt của vật liệu bán dẫn như thế nào.
Cùng với việc mô tả mặt phẳng tinh thể trong mạng, chúng ta còn
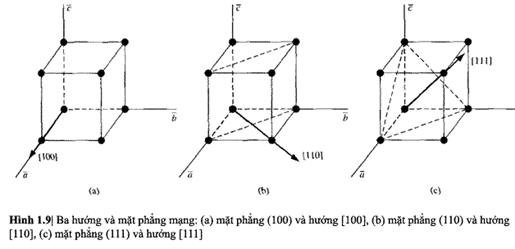
muốn mô tả những hướng đặc biệt trong tinh thể. Hướng có thể được biễu diễn qua
tập hợp 3 số nguyên là những thành phần tọa độ của một vecto theo hướng đó. Chẳng
hạn, đường chéo của mạng lập phương đơn sẽ có tọa độ là 1,1,1. Do đó, đường
chéo được mô tả theo hướng [111]. Dấu ngoặc vuông dùng để phân biệt với dấu ngoặc
tròn (được dùng để chỉ mặt phẳng mạng). Ba hướng cơ bản và những mặt phẳng mạng
có liên quan của cấu trúc lập phương đơn được biễu diễn trong hình 1.9. Chú ý rằng
trong mạng lập phương đơn, hướng [hkl] vuông góc với mặt phẳng (hkl). Tính chất
này sẽ không còn đúng trong mạng không phải lập phương.
1.3.4
Cấu trúc kim cương
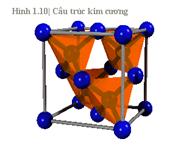 Như
đã từng nói, silic là một vật liệu bán dẫn phổ biến nhất. Silic là nguyên tố
nhóm IV và có cấu trúc kim cương. Germany cũng là một nguyên tố nhóm IV và có cấu
trúc giống kim cương. Ô đơn vị của kim cương được biễu diễn trong hình 1.10 phức
tạp hơn cấu trúc lập phương đơn mà chúng ta đã từng xem xét.
Như
đã từng nói, silic là một vật liệu bán dẫn phổ biến nhất. Silic là nguyên tố
nhóm IV và có cấu trúc kim cương. Germany cũng là một nguyên tố nhóm IV và có cấu
trúc giống kim cương. Ô đơn vị của kim cương được biễu diễn trong hình 1.10 phức
tạp hơn cấu trúc lập phương đơn mà chúng ta đã từng xem xét.
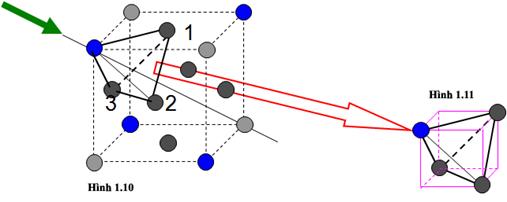
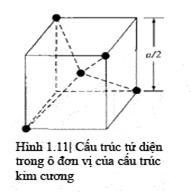 Chúng ta có thể bắt đầu hiểu mạng kim cương
bằng cách xem xét cấu trúc tứ diện được biễu diễn trong hình 1.11. Về cơ bản cấu
trúc này là lập phương tâm khối thiếu 4 nguyên tử ở các đỉnh.
Chúng ta có thể bắt đầu hiểu mạng kim cương
bằng cách xem xét cấu trúc tứ diện được biễu diễn trong hình 1.11. Về cơ bản cấu
trúc này là lập phương tâm khối thiếu 4 nguyên tử ở các đỉnh.
Mỗi nguyên tử trong cấu
trúc tứ diện có 4 nguyên tử lân cận gần nhất và cấu trúc này là thành phần cơ bản
của mạng kim cương.
Có một vài cách để hình dung cấu trúc kim cương. Một cách để hiểu
sâu hơn về cấu trúc kim cương là xét hình 1.12.
Hình 1.12a biễu diễn 2
cấu trúc lập phương tâm khối, hoặc tứ diện, những cấu trúc này kề chéo nhau. Những
vòng tròn tô đen biễu diễn những nguyên tử trong mạng được tạo ra khi cấu trúc
được tịnh tiến sang trái hoặc sang phải một hằng số mạng a.
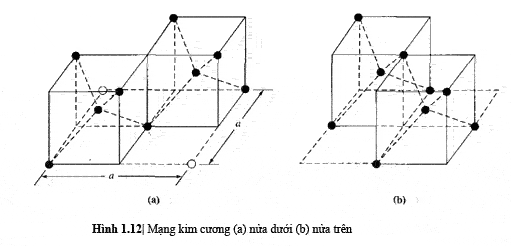 Hình
1.12b biễu diễn nửa trên của cấu trúc kim cương. Nửa trên chứa 2 cấu trúc tứ diện
được nối chéo nhau theo một đường vuông góc với đường chéo nửa dưới. Một tính
chất quan trọng trong cấu trúc kim cương là bất kì nguyên tử nào trong cấu trúc
kim cương cũng có 4 nguyên tử lân cận gần nhất. Chúng ta sẽ rút ra tính chất
này một lần nữa khi nghiên cứu về liên kết nguyên tử trong phần tiếp theo.
Hình
1.12b biễu diễn nửa trên của cấu trúc kim cương. Nửa trên chứa 2 cấu trúc tứ diện
được nối chéo nhau theo một đường vuông góc với đường chéo nửa dưới. Một tính
chất quan trọng trong cấu trúc kim cương là bất kì nguyên tử nào trong cấu trúc
kim cương cũng có 4 nguyên tử lân cận gần nhất. Chúng ta sẽ rút ra tính chất
này một lần nữa khi nghiên cứu về liên kết nguyên tử trong phần tiếp theo.
![]()